кандидат физико-математических наук,
старший научный сотрудник
Дом физических проблем, г. Ташкент, Узбекистан
t.z.kalanov@rambler.ru
Анализ проблемы соотношения геометрии и естествознания
Аннотация. Работа посвящена анализу актуальной проблемы – проблемы соотношения геометрии и естествознания. Методологическим базисом анализа является единство формальной логики и рациональной диалектики. В рамках этого базиса показывается, что геометрия представляет собой раздел естествознания. Сформулированы определения основных понятий элементарной (евклидовой) геометрии – «точка», «линия», «прямая линия», «поверхность», «плоская поверхность», «треугольник». Предлагаются естественнонаучное доказательство аксиомы параллельности (пятого постулата Евклида), классификация треугольников на основе качественного (существенного) признака, а также материальная интерпретация геометрий Евклида, Лобачевского, Римана.
Ключевые слова: геометрия, философия науки
Введение
Науки отличаются друг от друга тем, что они абстрагируют разные стороны реальности. Общей теоретической основой всех наук является единство формальной логики и рациональной диалектики (философского формализма), а критерием истинности – практика (т.е. материальная деятельность людей). Математика занимает особое место среди других наук: она абстрагирует общий аспект реальности – количественные отношения, которые возникают в процессе измерений свойств материальных объектов. Очевидно, что свойства, признаки (например, энергия, масса, скорость, протяженность, поверхность, плоскость, кривизна, окружность, прямолинейность и т.д.) объектов не существуют независимо от самих объектов: существуют не качества и количества, а только объекты, обладающие качествами и количествами. Поэтому критерий истинности чистой математики (т.е. математики, отвлеченной от свойств материальных объектов) не находится в ней самой. Он находится в естественных науках, изучающих свойства материальных объектов. Естественные науки используют чистую математику путем ее материальной интерпретации (приложения). Критерием истинности интерпретированной (прикладной) математики является практика.
Как известно, проблема соотношения геометрии и естествознания – настоятельная проблема философии и естествознания 21 века – не была решена в 20 веке. Это объясняется тем, что исследования по основаниям геометрии, выполненные Н. Лобачевским (N. Lobachevski), Я. Больяем (Janos Bolyai), Б. Риманом (B. Riemann), Д. Гильбертом (D. Hilbert), Ф. Клейном (F. Klein), Дж. Д. Биркгоффом (G. D. Birkhoff), А. Тарским (A. Tarski) и др. в 19-20 веках, и создание теории относительности А. Эйнштейном (A. Einstein) в 20 веке привели к возникновению двух точек зрения на геометрию. Традиционное понимание геометрии в смысле «Начал» (“Elements”) Евклида, существовавшее более двух тысяч лет, раздвоилось на противоположные аспекты: математический (абсолютный) аспект и физический (относительный) аспект. Эти аспекты можно охарактеризовать следующим образом.
1. В 19 веке возникла и стала общепринятой «абсолютная геометрия», т.е. современная математическая (абсолютная, логическая, нефилософская, оторванная от практики) точка зрения, с которой в настоящее время рассматриваются геометрические понятия и геометрические аксиомы [1]. В отличие от «Начал» Евклида, в современных списках аксиом евклидовой геометрии нет описаний геометрических объектов (т.е. нет определений понятий геометрических объектов). Предполагается, что существуют три группы предметов, называемых «точками», «прямыми» и «плоскостями», относительно которых соблюдены некоторые вполне определенные условия. Предметы, о которых идет речь в аксиомах, и отношения между этими предметами могут быть выбраны как угодно, с соблюдением только требований аксиом. Другими словами, современная геометрия разрывает связь теории и практики: современная геометрия оперирует понятиями, которые выражают некоторые свойства объектов, отделенные (абстрагированные) от самих объектов. Поэтому современная геометрия не может ответить на следующий важный вопрос: Почему аксиома V (аксиома параллельности) не является следствием аксиом I–IV в списке аксиом Гильберта [2]? Чтобы ответить на этот вопрос, следует учесть два существенных обстоятельства. Во-первых, с рационально-диалектической точки зрения, нельзя абстрагировать свойства от объектов – носителей этих свойств, – потому что свойства объектов не существуют отдельно от самих объектов. Во-вторых, с формально-логической точки зрения, список аксиом Гильберта не является корректным и полным, потому что он не содержит определений основных геометрических понятий – «точка», «линия», «прямая линия», «поверхность», «плоская поверхность». «треугольник».
2. В 20-м веке возник современный физический (относительный, логический, философский, связанный с практикой) подход к пониманию сущности геометрии. Он был предложен Эйнштейном в связи с созданием теории относительности. Несмотря на ошибочность теории относительности [3], подход Эйнштейна не противоречит смыслу «Начал» Евклида и состоит в следующем: «Из всех наук математика пользуется особым уважением, потому что ее теоремы абсолютно верны и неоспоримы, тогда как законы других наук в известной степени спорны и всегда существует опасность их опровержения новыми открытиями. Однако положения математики покоятся не на реальных объектах, а исключительно на объектах нашего воображения. В связи с этим возникает вопрос, который волновал исследователей всех времен. Почему возможно такое превосходное соответствие математики с реальными предметами, если сама она является произведением только человеческой мысли, не связанной ни с каким опытом? Может ли человеческий разум без всякого опыта, путем только одного размышления понять свойства реальных вещей? На мой взгляд, ответ на этот вопрос вкратце таков: если теоремы математики прилагаются к отражению реального мира, они не точны; они точны до тех пор, пока они не ссылаются на действительность. Сама по себе математика ничего не может сказать о реальных объектах. Однако, с другой стороны, верно и то, что математика вообще и геометрия в частности обязаны своим происхождением необходимости узнать что-либо о поведении реально существующих предметов. Ясно, что из системы понятий аксиоматической геометрии нельзя получить никаких суждений о таких реально существующих предметах, которые мы называем практически твердыми телами. Чтобы такого рода суждения были возможны, мы должны лишить геометрию ее формально-логического характера, сопоставив пустой схеме понятий аксиоматической геометрии реальные объекты нашего опыта. Для этой цели достаточно прибавить только такое утверждение: твердые тела ведут себя в смысле различных возможностей взаимного расположения, как тела евклидовой геометрии трех измерений; таким образом, теоремы евклидовой геометрии содержат в себе утверждения, определяющие поведение практически твердых тел. Дополненная таким утверждением, геометрия становится, очевидно, естественной наукой; мы можем рассматривать ее фактически как самую древнюю ветвь физики. Ее утверждения покоятся существенным образом на выводах из опыта, а не только на логических заключениях. Будем в дальнейшем называть дополненную таким образом геометрию «практической геометрией» в отличие от «чисто аксиоматической геометрии» [4]. Однако подход Эйнштейна не был корректно проанализирован и обоснован в работах современных ученых (например, в работе Адольфа Грюнбаума (Adolf Grünbaum) [5]). Кроме того, этот подход не является общепринятым, потому что он не содержит методологического ключа к решению проблемы соотношения геометрии и естествознания.
Поэтому цель настоящей работы состоит в том, чтобы предложить анализ проблемы соотношения геометрии и естествознания в рамках корректного методологического базиса – единства формальной логики и рациональной диалектики.
1. Методологический базис анализа
Принцип единства формальной логики (т.е. науки о законах правильного мышления) и рациональной диалектики (т.е. диалектики, основанной на рациональном мышлении) представляет собой методологический базис корректного анализа. Методологический базис содержит общие аргументы (предпосылки) для дедуктивного доказательства теоретических положений. Общие аргументы (предпосылки) состоят в следующем.
1. В соответствии с принципом материальности природы, природа – это система материальных объектов (частиц, полей, тел). Исследование систем проводится в рамках системного подхода. Системный подход – направление методологии научного познания, в основе которого лежит рассмотрение объектов как систем. Системный подход является конкретизацией основных принципов рациональной диалектики.
2. Система (т.е. целое, составленное из частей; соединение) – это множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство. Выделяют материальные и абстрактные системы. В современной науке исследования систем разного рода проводится в рамках различных специальных теорий систем.
3. В соответствии с рациональной диалектикой, материальный объект имеет качественную и количественную определенности (т.е. качественный и количественный аспекты). Единство качественной и количественной определенностей (аспектов) объекта называется свойством (мерой) объекта (например, физическое, химическое, геометрическое свойства). Свойства, признаки (например, энергия, масса, скорость, протяженность, поверхность, плоскость, кривизна, окружность, прямолинейность и т.д.) объектов не существуют независимо от самих объектов: существуют не качества и количества, а только объекты, обладающие качествами и количествами. Другими словами, свойство (мера) является неотъемлемой характеристикой материального объекта и принадлежат только материальному объекту.
4. Чистая математика изучает количественную определенность, отделенную (абстрагированную) от качественной определенности (т.е. от свойств, признаков) материального объекта. Поэтому чистая математика не имеет качественного (например, физического, химического, геометрического) смысла. Критерий истинности чистой математики не находится в ней самой. Он находится в естественных науках, изучающих материальные объекты. Эти науки используют чистую математику путем ее материальной интерпретации (приложения). Материальная интерпретация состоит в том, что устанавливается отношение тождества между понятиями «материальный объект» и «математический объект». Критерием истинности интерпретированной (прикладной) математики является практика.
5. Естественные науки изучают свойства (меру) материальных объектов (например, физические, химические, геометрические свойства). Математический аппарат (математический формализм) является средством количественного изучения материальных объектов. Прикладная математика (т.е. математика, приложенная к изучению материальных объектов) приводит к математическим соотношениям естественных наук. Математические соотношения естественных наук описывают свойства материальных объектов, содержат ссылку на эти объекты и поэтому имеют качественный (естественнонаучный) смысл. С формально-логической точки зрения, математические (количественные) операции над уравнением не приводят к изменению качественной определенности.
6. С формально-логической точки зрения, естественнонаучное понятие и математическое понятие можно сравнивать между собой только в том случае, если существуют логические отношения (например, отношение тождества) между ними. Поэтому приложение математики к описанию (изучению) свойств материального объекта возможно только в том случае, если используемые математические понятия тождественны используемым естественнонаучным понятиям, т.е. если между естественнонаучными понятиями (характеризующими материальный объект) и математическими понятиями (характеризующими математический объект) установлено отношение тождества.
7. Описание качественной и количественной определенностей (аспектов) материального объекта подчиняется законам формальной логики. Согласно закону тождества, левая и правая части математического уравнения должны принадлежать одной и той же качественной определенности (аспекту) материального объекта. А согласно закону противоречия, левая и правая части математического уравнения не должны принадлежать разным качественным определенностям (аспектам) материального объекта.
8. Материальный объект имеет множество свойств. Если форма макроскопического объекта (т.е. соотношение размеров и взаимное расположение частей макроскопического объекта) представляет собой единственный существенный признак объекта, то макроскопический объект называется геометрическим объектом (телом). С этой точки зрения, геометрия (как наука о геометрических свойствах системы материальных объектов) – это не часть (раздел) математики. Сущность геометрии состоит в том, что геометрия – это раздел естествознания, изучающий геометрические свойства системы макроскопических материальных объектов посредством теории систем и математики. (Используемый в геометрии метод построения (конструирования, синтеза) как способ изучения не является математикой). Например, геометрия является составной частью науки о прочности и деформируемости элементов сооружений и деталей машин [6]. Основы этой инженерной науки были сформулированы Галилео Галилеем (Galileo Galilei) в его книге «Discorsi e Dimostrazioni matematiche» (Лейден, 1638), Леонардом Эйлером (L. Euler) и многими другими учеными.
9. Изучение геометрических свойств основывается на применении теории систем и математики. Основное положение теории систем формулируется следующим образом: свойства системы не являются следствием свойств ее элементов. С формально-логической точки зрения, применение математики допускается законом тождества только в том случае, если между понятиями «геометрический объект (тело)» и «математический объект» существует отношение тождества.
10. Одно из первых и важных условий применения математики к описанию геометрического тела состоит в том, что необходимо установить отношение тождества между математическим понятием «нуль» и геометрическим понятием «нулевой объект (тело)». Другими словами, необходимо определить понятие «нулевой объект (тело)» и рассматривать макроскопический «нулевой объект (тело)» как начало отсчета формы. Поскольку материальный объект имеет три измерения, то и геометрический объект (тело) представляет собой соотношение трех размеров.
11. Движение – это изменение вообще. Движение материального объекта – это переходы объекта из одних состояний в другие. Существуют физические, химические, геометрические и другие состояния материального объекта. В общем случае, окружающая среда оказывает влияние (воздействие) на состояния объектов. Множество геометрических состояний материального объекта называется геометрическим пространством объекта.
12. Если влиянием окружающей среды можно пренебречь, то форма материального объекта инвариантна относительно положения этого объекта в среде. В этом случае, геометрические состояния (т.е. геометрическое пространство) этого объекта есть просто положения этого объекта по отношению к другим объектам. Это геометрическое пространство называется евклидовым пространством объекта.
13. Если окружающая среда (физические поля) оказывает силовое воздействие на форму материального объекта, то материальный объект может принимать множество форм (геометрических состояний). В этом случае, геометрические состояния этого объекта представляют собой неевклидово пространство.
14. Аксиоматическое построение науки – современный этап развития рационального мышления. Аксиома – элементарное положение теории, выражающее эмпирический (экспериментальный) факт.
Сформулированные аргументы (предпосылки) позволяют определить основные понятия геометрии.
2. Определение основных понятий элементарной геометрии
Основные понятия элементарной (евклидовой) геометрии – «точка», «линия», «поверхность» – определяются следующим образом.
1. Понятие «геометрический объект (тело)» выражает существенный признак материального объекта. Это – общее и конкретное понятие. Объем общего понятия выражается в виде логического класса. Этот класс является высшим классом (т.е. родом).
2. Точка – это «материальная точка», «нулевой объект (тело)». «Материальная точка», «нулевой объект (тело)» – это геометрический объект (т.е. макроскопическое тело или макроскопическая часть тела), три размера которого считаются (всегда принимаются, предполагаются) равными нулю. «Нулевой объект (тело)» не делится на части (т.е. не имеет частей) и представляет собой начало отсчета формы. Понятие «точка» – это видовое и конкретное понятие. «Ненулевой геометрический объект (тело или часть тела)» содержит множество точек и поэтому является геометрическим местом точек.
3. Линия – это геометрический объект (тело или часть тела), два размера которого считаются (принимаются, предполагаются) равными нулю. Понятие «линия» – это видовое и конкретное понятие. Это понятие не содержит утверждения о способе упорядочения точек линии.
4. Поверхность – это геометрический объект (тело или поверхностная часть (слой) тела), один размер которого считается (принимается, предполагается) равным нулю. Понятие «поверхность» – это видовое и конкретное понятие. Это понятие не содержит утверждения о способе упорядочения точек поверхности.
Эти основные понятия позволяют определить производные (подчиненные) понятия «плоскость» («плоская поверхность»), «окружность», «прямая линия». Как известно, общая форма логического определения понятий – это определение через ближайший род и видовое отличие. Общая форма определения является полной формой определения, если видовое отличие может быть определено. Видовые понятия «плоскость» («плоская поверхность»), «окружность», «прямая линия» могут быть определены только посредством генетического определения. Согласно формальной логике, генетическое определение – это особый вид определения, показывающий, как возникает данный объект. Поэтому генетические определения понятий «плоскость» («плоская поверхность»), «окружность», «прямая линия» должны показывать, как возникает упорядоченность точек прямой линии, окружности и плоской поверхности. Генетические определения основных понятий состоят в следующем.
(а) Плоскость (плоская поверхность) – это поверхность, которая возникает как геометрическое место точек при расположении этих точек на равном (одинаковом) расстоянии от двух фиксированных точек-полюсов, не принадлежащих поверхности. Другими словами, плоскость – это поверхность, представляющая собой геометрическое место точек, равноудаленных от двух точек-полюсов, не принадлежащих поверхности. Эти точки-полюса называются полюсами плоскости.
(б) Часть плоскости, ограниченная круговой линией, называется кругом. Круговая линия (окружность) – это замкнутая кривая линия, которая возникает как геометрическое место точек на плоскости при расположении этих точек на равном (одинаковом) расстоянии от одной фиксированной точки-полюса, принадлежащей плоскости. Другими словами, окружность (круговая линия) – это замкнутая кривая линия, представляющая собой геометрическое место точек плоскости, равноудаленных от одной точки-полюса, принадлежащей плоскости. Эта точка-полюс называется полюсом (или центром) окружности. Между окружностью и ее полюсом существует следующее отношение: полюс определяет (порождает) множество непересекающихся (концентрических) окружностей; порожденная окружность характеризует один и только один полюс. Часть плоскости, ограниченная окружностью, называется кругом. Следствия: существование системы «плоскость и один полюс на ней» представляет собой необходимое условие возникновения (существования) окружности (круговой линии) и круга; окружность (круговая линия) – носитель свойства кривизны; свойство кривизны – это одно из проявлений свойств системы «плоскость и один полюс на ней»; понятие «кривизна» – абстрактное понятие.
(в) Прямая (прямая линия) – это линия, которая возникает как геометрическое место точек на плоскости при расположении этих точек на равном (одинаковом) расстоянии от двух фиксированных точек-полюсов, принадлежащих плоскости. Другими словами, прямая – это линия, представляющая собой геометрическое место точек плоскости, равноудаленных от двух точек-полюсов, принадлежащих плоскости. Эти точки-полюса называются полюсами прямой линии. Между прямой линией и ее полюсами существует следующее отношение: заданная пара полюсов определяет (порождает) одну и только одну прямую линию; порожденная прямая линия характеризует геометрическое место полюсов. Следствия: существование системы «плоскость и две точки-полюса на ней» представляет собой необходимое условие возникновения (существования) прямой линии; две произвольные точки плоскости определяют прямую линию (другими словами: прямая линия проходит через две произвольные точки; через две произвольные точки можно провести одну и только одну прямую линию); прямая линия – носитель свойства прямизны; свойство прямизны – это одно из проявлений свойств системы «плоскость и два полюса на ней»; понятие «прямизна» – абстрактное понятие.
3. Свойства системы геометрических объектов
Элементарные геометрические объекты – точка, прямая линия, окружность, плоскость – являются элементами синтезированных геометрических объектов (систем): плоских углов, треугольников и т.д. Свойства синтезированной системы не являются логическим следствием свойств элементов. Поэтому изучение синтезированной системы состоит в экспериментальном определении свойств этой системы. С этой точки зрения, свойства системы выражаются в форме аксиом. Аксиомы – это элементарные теоретические положения, выражающие эмпирически (экспериментально) изученные свойства системы.
3.1. Плоский угол как система двух пересекающихся прямых линий
Если две прямые линии (элементы) на плоскости
соединяются (связываются) общей точкой, (т.е. точкой, через которую проходят
обе прямые линии), то синтезированная система (построенная, сконструированная
геометрическая фигура) называется плоским углом. Точка соединения (пересечения)
прямых линий называется вершиной угла, а прямые линии, ограниченные вершиной,
– сторонами угла. Мерой угла являются градусы или радианы. Нулевым углом
(имеющим меру ![]() ,
или
,
или ![]() )
называется угол, стороны которого совпадают (совмещены). Развернутым углом
(имеющим меру
)
называется угол, стороны которого совпадают (совмещены). Развернутым углом
(имеющим меру ![]() ,
или
,
или ![]() )
называется угол, стороны которого образуют прямую линию. Прямым углом (имеющим
меру
)
называется угол, стороны которого образуют прямую линию. Прямым углом (имеющим
меру ![]() ,
или
,
или ![]() )
называется угол, величина которого равна половине развернутого угла. Основное
свойство угла как системы состоит в следующем: величина угла не зависит от
длины его сторон (элементов).
)
называется угол, величина которого равна половине развернутого угла. Основное
свойство угла как системы состоит в следующем: величина угла не зависит от
длины его сторон (элементов).
3.2. Параллельные прямые линии как подсистема
Если: (а) прямая линия, проходящая через две точки плоскости, представляет собой геометрическое место полюсов прямых линий; (б) один из полюсов фиксирован, а другой является переменным, – то на плоскости существует множество (система) прямых линий, определяемых (порождаемых) переменным полюсом. Все эти прямые линии связаны отношением параллельности.
Две прямые линии связаны отношением параллельности и
называются параллельными, если расстояние ![]() между ними представляет собой
разность расстояний полюсов
между ними представляет собой
разность расстояний полюсов ![]() -ой и
-ой и ![]() -ой прямых линий:
-ой прямых линий: ![]() ,
, ![]() , где
, где ![]() и
и ![]() – расстояния
полюсов
– расстояния
полюсов
![]() -ой и
-ой и ![]() -ой прямых линий
соответственно. Поскольку
-ой прямых линий
соответственно. Поскольку ![]() при
при ![]() , то параллельные прямые совпадают (совмещаются) при
, то параллельные прямые совпадают (совмещаются) при ![]() .
.
Следствия: (1) отношение параллельности двух заданных прямых линий устанавливается посредством третьей прямой линии, проходящей через полюса и связывающей (пересекающей) эти две прямые линии; параллельные линии образуют прямой угол с линией, проходящей через полюса; (2) отношение параллельности двух прямых линий – это свойство системы трех прямых линий; (3) параллельные прямые линии не пересекаются; (4) если: прямая линия, проходящая через две точки плоскости, является единственной и представляет собой геометрическое место полюсов параллельных прямых линий; любой точке, не лежащей на геометрическом месте полюсов, соответствуют фиксированные полюса; фиксированные полюса определяют единственную прямую линию, – то через произвольную точку плоскости проходит одна и только одна прямая линия, параллельная данным параллельным прямым линиям (это утверждение выражает свойство инвариантности прямого угла при движении).
Таким образом, эти следствия выражают экспериментально изученные свойства системы. Элементарные теоретические положения, выражающие экспериментально изученные свойства системы, являются аксиомами. Это означает, что V аксиома Гильберта (аксиома параллельности) [2] не является логическим следствием аксиом I–IV потому, что свойство системы геометрических элементов не является следствием свойств ее элементов.
3.3. Треугольник как система трех пересекающихся прямых линий
Если
стороны плоского угла соединяются (связываются) прямой линией, то
синтезированная система (построенная геометрическая фигура) называется
треугольником. Точки пересечения прямых линий (т.е. три точки ![]() ,
, ![]() ,
, ![]() ) называются
вершинами треугольника, а прямые линии (т.е. три прямые линии – отрезки
) называются
вершинами треугольника, а прямые линии (т.е. три прямые линии – отрезки ![]() ,
, ![]() ,
, ![]() ), ограниченные
вершинами, – сторонами треугольника. Существование внутренних углов (т.е.
элементов
), ограниченные
вершинами, – сторонами треугольника. Существование внутренних углов (т.е.
элементов ![]() ,
,
![]() ,
, ![]() ) треугольника
приводит к возникновению существенного признака (параметра) системы: суммы
) треугольника
приводит к возникновению существенного признака (параметра) системы: суммы ![]() . Значение
. Значение ![]() можно
определить только посредством экспериментального изучения свойств треугольника
как системы.
можно
определить только посредством экспериментального изучения свойств треугольника
как системы.
Экспериментальное устройство представляет собой
следующую материальную конструкцию: материальный треугольник, вершинами ![]() ,
, ![]() ,
, ![]() которого
являются шарниры. Шарниры позволяют изменять параметры элементов: величины
(значения) углов
которого
являются шарниры. Шарниры позволяют изменять параметры элементов: величины
(значения) углов ![]() ,
, ![]() ,
, ![]() и длины сторон треугольника. (Другими
словами, шарниры допускают структурное («внутреннее») движение треугольника
(т.е. переходы из одних структурных состояний в другие). Структурное движение
треугольника сводится к двум элементарным движениям его сторон: «сдвигу вдоль
прямой линии» и «вращению вокруг точки»). Постановка проблемы состоит в
следующем: необходимо показать экспериментально, что свойство
и длины сторон треугольника. (Другими
словами, шарниры допускают структурное («внутреннее») движение треугольника
(т.е. переходы из одних структурных состояний в другие). Структурное движение
треугольника сводится к двум элементарным движениям его сторон: «сдвигу вдоль
прямой линии» и «вращению вокруг точки»). Постановка проблемы состоит в
следующем: необходимо показать экспериментально, что свойство ![]() треугольника
(как системы) не зависит от свойств (параметров) элементов треугольника.
(Другими словами, необходимо показать, что
треугольника
(как системы) не зависит от свойств (параметров) элементов треугольника.
(Другими словами, необходимо показать, что ![]() является инвариантом структурного
движения треугольника).
является инвариантом структурного
движения треугольника).
Результаты эксперимента состоят в следующем:
(а)
если ![]() –
независимая переменная величина, то
–
независимая переменная величина, то ![]() – линейная функция
– линейная функция ![]() ;
; ![]() ;
;
(б)
если ![]() ,
то
,
то ![]() ;
;
(в)
если ![]() ,
то
,
то ![]() ;
;
(г)
![]() ;
;
(д) площадь (как переменная величина) не является существенным признаком треугольника;
(е) в отличие от рассуждений Лежандра (A.M. Legendre), в эксперименте не предполагается, что «стороны в треугольнике растут бесконечно» (Н. Лобачевский) [6]. Поэтому можно «заключить отсюда, что с уменьшением двух углов, приближение противоположных сторон к третьей оканчивается необходимо превращением остального угла в два прямые» (Н. Лобачевский) [6].
Результаты эксперимента означают, что ![]() представляет
собой сумму смежных углов
представляет
собой сумму смежных углов ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() .
.
Таким образом, свойство прямолинейного треугольника
как системы состоит в том, что сумма ![]() внутренних углов прямолинейного треугольника
равна
внутренних углов прямолинейного треугольника
равна ![]() и
не зависит от свойств его элементов, т.е.
и
не зависит от свойств его элементов, т.е. ![]() является инвариантом движения прямолинейного
треугольника. Этот экспериментальный факт представляет собой эквивалент V-го
постулата Евклида (или аксиомы V в списке аксиом Гильберта).
является инвариантом движения прямолинейного
треугольника. Этот экспериментальный факт представляет собой эквивалент V-го
постулата Евклида (или аксиомы V в списке аксиом Гильберта).
4. Естественнонаучная классификация треугольников и геометрий
Как
известно, в основе общепринятой математической классификации геометрий лежит не
качественная определенность треугольника, а количественная определенность –
значение суммы ![]() внутренних углов плоского
треугольника:
внутренних углов плоского
треугольника: ![]() (геометрия
Евклида),
(геометрия
Евклида), ![]() (геометрия Лобачевского),
(геометрия Лобачевского), ![]() (геометрия
Римана). С формально-логической точки зрения, такая классификация является
некорректной, а естественнонаучная классификация треугольников на основе
качественной определенности (существенного признака) является корректной.
Корректная классификация треугольников представляет собой ключ к
естественнонаучной (материальной) интерпретации геометрий Евклида,
Лобачевского, Римана.
(геометрия
Римана). С формально-логической точки зрения, такая классификация является
некорректной, а естественнонаучная классификация треугольников на основе
качественной определенности (существенного признака) является корректной.
Корректная классификация треугольников представляет собой ключ к
естественнонаучной (материальной) интерпретации геометрий Евклида,
Лобачевского, Римана.
Классификация треугольников на основе существенного признака – качественной определенности сторон треугольника – производится следующим образом.
1. Определяются понятия линии, отрезка линии (элемента) и треугольника.
2. Класс линий делится на два непересекающихся класса: класс прямых линий и класс не-прямых линий. (Деление производится на основе признака кривизны: если линия не обладает признаком кривизны, то она является прямой; если линия обладает признаком кривизны, то она является кривой).
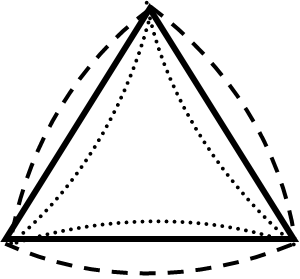
3. Класс треугольников делится на два непересекающихся класса: класс прямолинейных треугольников и класс не-прямолинейных (криволинейных) треугольников (Фиг. 1).
4. Треугольник является прямолинейным, если все его стороны образованы отрезками прямой линии (Фиг. 1).
5. Треугольник является не-прямолинейным (криволинейным), если хотя бы одна его сторона образована отрезком кривой линии.
6. Класс криволинейных треугольников делится на два непересекающихся подкласса: подкласс плоских и подкласс не-плоских криволинейных треугольников (Фиг. 1).
7. Подкласс плоских криволинейных треугольников делится на три подкласса: два непересекающихся подкласса (подкласс выпуклых и подкласс не-выпуклых (вогнутых) криволинейных треугольников) и один смешанный подкласс (Фиг. 1).
Вышеприведенная классификация является основой для экспериментального изучения количественной определенности треугольников. В соответствии с экспериментальными данными, справедливы следующие утверждения (Фиг. 1):
(а)
сумма внутренних углов любого треугольника есть либо ![]() , либо
, либо ![]() ;
;
(б)
сумма внутренних углов прямолинейного треугольника удовлетворяет соотношению: ![]() ;
;
(в)
сумма внутренних углов плоского вогнутого криволинейного треугольника
удовлетворяет соотношению ![]() ;
;
(г)
сумма внутренних углов плоского выпуклого криволинейного треугольника
удовлетворяет соотношению ![]() ;
;
(д)
сумма внутренних углов плоского выпукло-вогнутого криволинейного треугольника,
относящегося к смешанному подклассу, может удовлетворять любому из
соотношений: ![]() ,
, ![]() ,
, ![]() .
.
|
Фиг. 1. Основные типы плоских треугольников: прямолинейный треугольник (изображен
сплошной линией),
|
Эти утверждения могут быть кратко сформулированы в виде следующей теоремы о сумме внутренних углов плоского треугольника.
Теорема. Если плоский
треугольник является прямолинейным, то ![]() ; если
плоский треугольник является вогнутым, то
; если
плоский треугольник является вогнутым, то ![]() ; если
плоский треугольник является выпуклым, то
; если
плоский треугольник является выпуклым, то ![]() .
.
Обратная теорема не верна.
Таким образом, понятия «геометрия прямолинейного треугольника», «геометрия плоского вогнутого треугольника» и «геометрия плоского выпуклого треугольника» тождественны понятиям «геометрия Евклида», «геометрия Лобачевского» и «геометрия Римана» соответственно.
5. Естественнонаучный (инженерный) смысл функции Лобачевского
Как известно, фундаментальную роль в неевклидовой геометрии играет функция Лобачевского [1]. Для выяснения естественнонаучного (материального, инженерного) смысла функции Лобачевского следует рассмотреть деформацию бесконечного прямолинейного стержня (Фиг. 2).
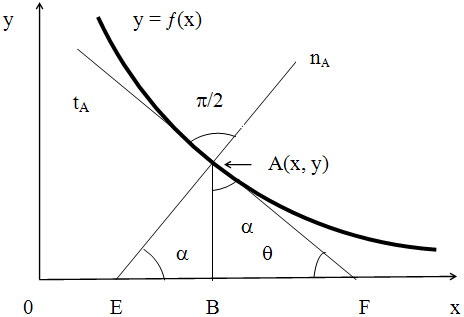
Фиг. 2. Деформация стержня и функция Лобачевского:
|
![]() Пусть, в соответствии с курсом «Сопротивление материалов» [7],
выполняются следующие условия:
Пусть, в соответствии с курсом «Сопротивление материалов» [7],
выполняются следующие условия:
1) при действии внешних сил происходит плоский изгиб стержня;
2)
прямая задача состоит в нахождении уравнения изогнутой оси стержня: ![]() ;
;
3)
деформация полностью определяется положением поперечного сечения стержня в
произвольной точке ![]() линии
линии ![]() ;
;
4)
положение поперечного сечения стержня в точке ![]() полностью определяется следующими
величинами: (а) прогибом стержня – перпендикуляром
полностью определяется следующими
величинами: (а) прогибом стержня – перпендикуляром ![]() к оси
к оси
![]() , т.е.
координатой
, т.е.
координатой ![]() точки
точки
![]() ; (б)
углом
; (б)
углом ![]() поворота
поперечного сечения в точке
поворота
поперечного сечения в точке ![]() , т.е. углом
, т.е. углом ![]() , образованным осью
, образованным осью ![]() и касательной
и касательной ![]() в
точке
в
точке ![]() :
:
![]() ;
;
5)
в прямоугольном треугольнике ![]() угол
угол ![]() является функций
является функций ![]() , т.е.
в каждой точке
, т.е.
в каждой точке ![]() существует определенная зависимость между
существует определенная зависимость между ![]() и
и ![]() ;
;
6)
функция ![]() монотонна
и непрерывна;
монотонна
и непрерывна;
7)
угол ![]() связан
с углом
связан
с углом ![]() ,
образованным осью
,
образованным осью ![]() и нормалью
и нормалью ![]() к оси стержня
в точке
к оси стержня
в точке ![]() ,
соотношением:
,
соотношением: ![]() (т.е. в прямоугольном треугольнике
(т.е. в прямоугольном треугольнике ![]() угол
угол ![]() является
функцией
является
функцией ![]() );
);
8)
условия закрепления концов стержня имеют вид: ![]() при
при ![]() и
и
![]() при
при ![]() .
.
Тогда справедлива следующая теорема существования функции Лобачевского.
Теорема. Если функция
![]() определена для каждого положительного
определена для каждого положительного ![]() ,
монотонно убывает и непрерывна,
,
монотонно убывает и непрерывна, ![]() при
при
![]() и
и ![]() при
при
![]() , то
угол
, то
угол ![]() при
точке
при
точке ![]() является
углом параллельности по отношению к оси
является
углом параллельности по отношению к оси ![]() , а функция
, а функция ![]() представляет
собой функцию Лобачевского [3, 4].
представляет
собой функцию Лобачевского [3, 4].
Отсюда следует, что естественнонаучный (материальный, инженерный) смысл функции Лобачевского состоит в том, что она характеризует положение поперечного сечения деформированного стержня.
6. Обсуждение
Понятия «геометрия Евклида», «геометрия Лобачевского», «геометрия Римана» обретают естественнонаучный смысл только в случае материальной интерпретации треугольников. Если принять во внимание существование окружающей среды, могущей оказывать силовое воздействие на материальный прямолинейный треугольник, и рассматривать полную систему «материальный прямолинейный треугольник + окружающая среда», то становится понятным, что воздействие внешних сил приводит к деформации (растяжению, сжатию, изгибу, кручению) сторон прямолинейного треугольника. При действии внешних сил, векторы которых лежат в плоскости прямолинейного треугольника, прямолинейный треугольник деформируется (Фиг. 1) и, следовательно, реализуется либо геометрия Лобачевского, либо геометрия Римана, либо геометрия смешанного типа. При действии внешних сил, векторы которых не лежат в плоскости прямолинейного треугольника, прямолинейный треугольник, деформируясь, превращается в не-плоский треугольник и, следовательно, реализуется «геометрия не-плоского треугольника». В отсутствие внешних сил прямолинейный треугольник не деформируется (Фиг. 1) и, следовательно, реализуется геометрия Евклида.
С точки зрения экспериментального исследования полной системы «материальный треугольник + окружающая среда», «вопрос о том, какова истинная геометрия Вселенной» [8], является некорректным. Действительно, поскольку прямолинейные треугольники могут быть образованы, например, световыми лучами, твердыми стержнями и т.д. (на которые внешняя среда оказывает различное влияние), то результаты экспериментального исследования будут представлять собой множество различных истинных геометрий: «геометрии треугольника, образованного световыми лучами», «геометрии треугольника, образованного твердыми стержнями» и т.д.
С естественнонаучной точки зрения, решение проблемы логической непротиворечивости геометрий Евклида, Лобачевского и Римана является тривиальным. Действительно, геометрии Евклида, Лобачевского и Римана взаимно непротиворечивы, потому что, в согласии с практикой, существование криволинейных треугольников Лобачевского и Римана не находится в противоречии с существованием прямолинейного треугольника Евклида.
И, наконец, о так называемой абсолютной геометрии. Как известно, абсолютная геометрия – это евклидова геометрия без пятого постулата [1]. Поэтому материальная сущность абсолютной геометрии – это «геометрия элементов» материальной системы: геометрия элементов «точка», «линия», «прямая линия», «поверхность».
Заключение
Таким образом, анализ проблемы соотношения геометрии и естествознания в рамках корректного методологического базиса – единства формальной логики и рациональной диалектики – показывает, что геометрия представляет собой раздел естествознания. Геометрия как раздел естествознания использует математический и философский аппараты (формализмы), а также опирается на эксперимент. Критерием истинности геометрических утверждений является практика. С этой точки зрения, практика представляет собой не только основу корректной классификации треугольников и геометрий, материальной интерпретации геометрий Евклида, Лобачевского, Римана, но и исходный пункт аксиоматического (системного) построения науки. Аксиоматическое построение науки – современный этап развития рационального мышления.
Рациональное мышление, основанное на единстве формальной логики и рациональной диалектики, приводит к новым результатам, полученным в настоящей работе. Эти результаты состоят в следующем.
1) Сформулированы генетические определения основных понятий элементарной (евклидовой) геометрии – «точка», «линия», «прямая линия», «поверхность».
2) Показано, что список аксиом Гильберта является неполным, потому что он не содержит определения понятия «треугольник».
3) Предложены естественнонаучное доказательство аксиомы параллельности (пятого постулата Евклида), классификация треугольников на основе качественного (существенного) признака, а также материальная интерпретация геометрий Евклида, Лобачевского, Римана.
Эти результаты имеют важное значение для выяснения сущности многомерной геометрии, а также для прогресса науки и техники.
Литература
[1] Н.В. Ефимов. Высшая геометрия. М.: Наука, 1978. 576 с.
[2] Д. Гильберт. Основания геометрии, Гостехиздат, 1948.
[3] T.Z. Kalanov, “Critical analysis of the special theory of relativity”, Bulletin of Pure and Applied Sciences, Vol. 26D, No 1 (2007), pp. 1-15
[4] А. Эйнштейн, “Геометрия и опыт”. Собрание научных трудов. Т. 2. М.: Наука, 1966. С. 83 – 94).
[5] A. Grünbaum. “Philosophical problems of space and time” (second edition, 1973).
[6] Н.И. Лобачевский. Избранные труды по геометрии. М.: Изд. Академии наук СССР, 1956. 596 с.
[8] Ч. Киттель, У. Найт, М. Рудерман. Механика. М.: Наука, 1975. 480 с.).