Способ трансформации и различения чисел
В статье рассмотрен «Способ нумерологической трансформации чисел», предназначенный для получения из любого исходного числа некоторого набора внутренне связанных с ним («порождённых») чисел с последующим (при необходимости) различением и анализом чисел для вскрытия неизвестных закономерностей и связей.
ПРАВИЛА ДЛЯ ДАННОГО СПОСОБА:
- Положение цифр в числе – не меняется
- Числа – «комбинаторные изонумы» здесь - не используются
- Меняется только группировка цифр а числах, начиная с исходного (скобками)
- Цифры в скобках складывают и результат вписывают в новое число.
- До нумерологических корней сокращения чисел на доводят.
- Затем все полученные числа выписывают и находят для них числа – зеркала.
- Для зеркальных чисел применяют ту же процедуру.
- Повторы чисел исключают
- Если получают (в скобках) числа более 9, то их тоже выписывают отдельно, как самостоятельные, а затем преобразуют по правилам 1 - 5.
- Выписывают все новые числа.
- Строят геометрию всех связей и превращений чисел. При этом исходное число – тоже исключается.
- Лимб для анализа берут по числу новых найденных чисел, т. е., для 7 новых чисел – берут Лимб-7 и т.д.
Сначала, для иллюстрации будем трансформировать число «147» -{147} – {12} – [3];
- 147 = (14)7 – 57
- 147 = 1(47) – 112
- 112 = (11)2 – 22
- 112 = 1(12) – 13
- Зеркала:
- 75
- 211
- 31
- 211 = 2(11) – 22
Итого, из числа: 147 получено 7 новых чисел: 57, 112, 22, 13, 75, 211, 31.
Общая сумма новых чисел: (57+112+22+13+75+211+31) = 521 – [8].
| Таблица 1 |
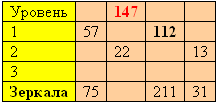 |
Теперь для сравнения будем трансформировать число «183» -- {183} – [3];
- 183= (18)9 -- 93
- 183 = 1(83) -- 111
- 111 = (11)1 -- 21
- 93 = (93) -- 12
- 111 = (11)1 -- 21
- 111 = 1(11) -- 12
Зеркала: 39, 111, 12
Прямые:93, 111, 21,
| Таблица 2 |
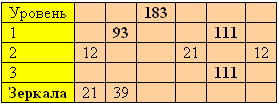 |
Итого, из числа 183 получены 5 новых чисел: 93, 111, 39, 12, 21.
Общая сумма новых чисел: (93+111+39+21+12) = 276 – [6].
ПРОМЕЖУТОЧНЫЕ ВЫВОДЫ:
О двух числах, проанализированных для иллюстрации метода - 183 и 147 и имеющих одинаковый нумерологический корень = [3], над которыми осуществлены одинаковые действия, можно сказать следующее:
- Таблицы трансформации их имеют совершенно разный, индивидуальный характер и вид
- Используемой процедурой (методом) можно РАЗЛИЧАТЬ числа, имеющие не только разные, но и одинаковые нумерологические корни.
Теперь построим лимб для чисел: 57, 112, 22, 13, 75, 211, 31,
(порождённых числом 147).
Это должен быть Лимб – 7 с нумерологическим сокращением «веса» (суммы чисел связей):
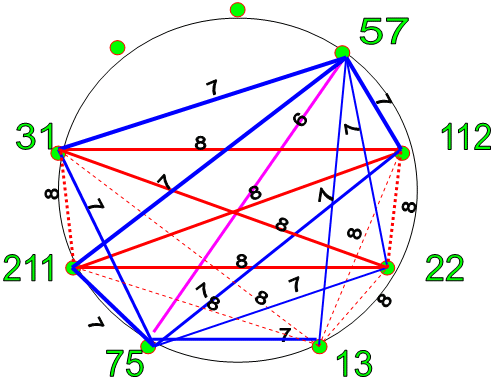 |
| Рис. 1 |
На полученном лимбе явственно преобладают цифры 7 и 8.
Красные линии вполне отчётливо формируют изображение Пирамиды (в изометрии)
- с основанием (31-112-22-211), Сумма: (143+134+233+242) = 752 =16х47
- с диагоналями: (31-22) и (211 –57). Суммы: (53+268) = 321 = 3х107;
- с вершиной – 13
- и рёбрами (31-13), (57-12), (22-1,), (211-13). Суммы: (44+69+23+224) = 360 = 4х90;
- ИТОГО: (752 + 360) = 1112 + 321 = 1433
Синие линии формируют два ортогональных (в изометрии) четырёхугольника:
- (57-31-75-112) . Сумма: ( 88 +106 +187 + 169) = 550 = 50х11
- ((57-211-75-13). Сумма: (268 + 286 + 88 +70) = 712 = 8х 89
- ИТОГО: 550 + 712 = 1262 = 2х 631
Выявленные простые числа выделены крупным жирным шрифтом и красным цветом:
11, 47, 89, 107, 631, 1433
В таблице сумм всех чисел (см. ниже) - красные числа – простые, а синие – простые составные.
| Таблица 3 |
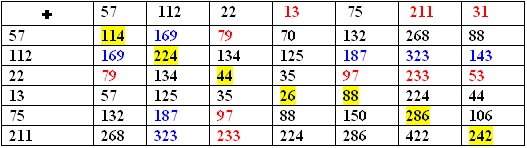 |
А, поскольку, при использовании данной процедуры (метода) можно РАЗЛИЧАТЬ не только разные числа, но и числа, имеющие одинаковые нумерологические корни, то для второго числа - «183» (см. Таблицу №2) нет необходимости строить свой лимб, поскольку он заведомо будет иным, а сопоставление лимбов – задачей данного исследования не являлось.
ИТОГ:
Итоги, иллюстрирующие работу данного способа, состоят в том, что для чисел, у которых одинаковы нумерологические корни, то есть для «изонумов» существует, в частности, метод их трансформации в наборы новых «порождённых» чисел с одновременной идентификацией различий.
Либо, при необходимости, с сопоставлением таких наборов для обоих «изонумов» (не комбинаторных).
|