Темур Зикириллаевич Каланов
кандидат физико-математических наук,
старший научный сотрудник
Дом физических проблем, г. Ташкент, Узбекистан
t.z.kalanov@rambler.ru
Распределение Больцмана: "Блоха в ухе физиков"
Аннотация. Статья посвящена актуальной проблеме - проблеме обоснованности теоретической физики. Показывается, что распределение Больцмана - одно из достижений статистической физики XIX века - не имеет ни статистического, ни физического смысла. Следовательно, понятие "распределение Больцмана" может и должно быть упразднено.
| |
"Часто ложные гипотезы оказывали больше услуг, чем верные"
(А. Пуанкаре) |
Введение
Несомненно, Л. Больцман, как и А. Эйнштейн, посадил «физикам в ухо большую блоху» (А. Эйнштейн). Сегодня эта «блоха» именуется распределением Больцмана. Распределение Больцмана представляет одно из достижений статистической физики XIX века и широко используется в теории идеального газа, лазерной физике, химической физике, физике плазмы и т.д. До настоящего времени больцмановское распределение не подвергалось серьезному сомнению, потому что физиков вполне устраивало следующее мнение: «Среди физиков довольно широко распространено заблуждение, что статистическая физика является наименее обоснованной областью теоретической физики. При этом обычно ссылаются на то, что некоторые выводы статистики доказываются не строго математически, и забывают, что и все другие области теоретической физики содержат столь же нестрогие доказательства, что, однако, не рассматривается как признак недостаточной обоснованности этих отделов. Между тем, работами Гиббса статистическая физика, основанная Клаузиусом, Максвеллом и Больцманом, была превращена в логически связанную и стройную систему. Гиббс дал общий метод, применимый принципиально ко всем задачам, которые могут быть поставлены перед статистической физикой. …Статистика и термодинамика образуют вместе единое целое. Все понятия и величины термодинамики наиболее естественно, просто и строго вытекают из понятий статистики. И если даже общие положения термодинамики и могут быть сформулированы без статистики, то их приложение к конкретным случаям требует, во всяком случае, применения статистики» (Л. Ландау и Е. Лифшиц. Статистическая физика. М.: Наука, 1976). Это мнение оказало магическое воздействие на поколение физиков XX века: в ярком свете этого мнения сомневающимся физикам стало мучительно стыдно за свое темное невежество, а тем временем не сомневающиеся физики бесстыдно и спешно делали карьеру, публикуя научные труды, защищая диссертации, создавая научные школы и плодя себе подобных. Все смирились с тем настораживающим фактом, что «вероятность термодинамическая не является вероятностью в математическом смысле» (Физический энциклопедический словарь). В результате, наука превратилась в лженауку, основными понятиями которой являются «термодинамическая вероятность», «распределение Больцмана», «населенность квантового уровня», «инверсия населенностей», «отрицательная температура» и др..
Таким образом, причиной серьезного сомнения в обоснованности статистической физики до сих пор остаются следующие общепринятые положения: (а) «Больцмана распределение представляет собой частный случай канонического распределения Гиббса для идеального газа» (Физический энциклопедический словарь); (б) «Вероятность термодинамическая не является вероятностью в математическом смысле; применяется в статистической физике для вычисления свойств системы, находящейся в термодинамическом равновесии» (Физический энциклопедический словарь). Цель настоящей статьи – показать, что распределение Больцмана не является следствием квантового канонического распределения Гиббса и не имеет физического смысла [1].
1. Квантовое каноническое распределение Гиббса
Как известно [1-4], понятие случайной величины должно быть исходным пунктом и основой статистической физической теории. В этом случае, распределение вероятностий дает правильное и полное описание физической системы [2, 3]. Если физической системой является «макроскопическая совокупность свободных квантовых частиц», она называется идеальным газом. Идеальный газ называется нормальным (не-квантовым) газом, если частицы «взаимодействуют только посредством взаимных столкновений» (Ейнштейн). А если частицы газа не взаимодействуют друг с другом, газ называется аномальным (квантовым). В случае тепловых являений в изолированной макроскопической системе «идеальный (нормальный) газ молекул», молекулы сталкиваются друг с другом случайным образом. Поскольку изменение энергии молекул происходит в результате большого числа случайных столкновений, то энергия молекулы представляет собой дискретную случайную величину. Если идеальный (нормальный) газ представить как систему «молекула + молекулярный газ» (где «молекула» - подсистема, а «молекулярный газ» - окружение), то справедливы следующие квантово-статистические утверждения [4].
1) Случайная величина принимает значения 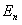 , , 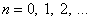 , где , где 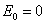 - начало отсчета значений случайной величины. - начало отсчета значений случайной величины.
2) Каждый элемент 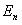 множества возможных значений энергии находится во взаимно однозначном соответствии с вероятностью множества возможных значений энергии находится во взаимно однозначном соответствии с вероятностью 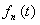 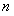 -го энергетического состояния молекулы. Распределение вероятностей -го энергетического состояния молекулы. Распределение вероятностей 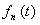 дает полное квантовостатистическое описание молекулы газа. дает полное квантовостатистическое описание молекулы газа.
3) Статистический ансамбль идентичных макроскопических систем «молекула в 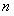 -ом квантовом состоянии + молекулярный газ» определяет вероятность -ом квантовом состоянии + молекулярный газ» определяет вероятность 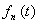 того, что молекула находится в того, что молекула находится в 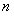 -ом квантовом состоянии с энергией -ом квантовом состоянии с энергией 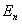 : :
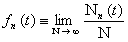 , , 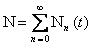 , , 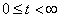 , ,
где 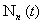 - число макроскопических систем «молекула в - число макроскопических систем «молекула в 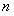 -ом квантовом состоянии + молекулярный газ» в момент времени -ом квантовом состоянии + молекулярный газ» в момент времени 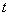 ; ; 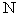 - полное число макроскопических систем «молекула + молекулярный газ» в ансамбле (это число не зависит от времени) - полное число макроскопических систем «молекула + молекулярный газ» в ансамбле (это число не зависит от времени)
4) Вероятность 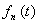 характеризует ансамбль систем и удовлетворяет условиям нормировки и консервативности нормировки характеризует ансамбль систем и удовлетворяет условиям нормировки и консервативности нормировки
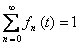 , , 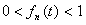 , ,
а также условиям однозначности и единственности.
5) Средне-статистическая энергия 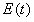 молекулы определяется соотношением молекулы определяется соотношением
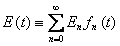 . .
6) Существует предел величины 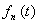 при при 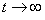 . Этот предел характеризует состояние статистического равновесия в макроскопической системе «молекула + молекулярный газ»: . Этот предел характеризует состояние статистического равновесия в макроскопической системе «молекула + молекулярный газ»:
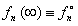 , , 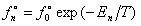
где 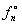 - квантовое каноническое распределение Гиббса, - квантовое каноническое распределение Гиббса, 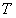 - статистическая температура молекулы (т.е. универсальный статистический параметр молекул, статистический потенциал системы). - статистическая температура молекулы (т.е. универсальный статистический параметр молекул, статистический потенциал системы).
7) Квантовое каноническое распределение Гиббса определяет корректное соотношение между средне-статистической (микроскопической энергией 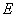 молекулы, средне-статистической (микроскопической) энтропией молекулы, средне-статистической (микроскопической) энтропией 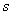 молекулы и статистической температурой молекулы и статистической температурой 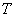 молекулы. Это соотношение имеет следующий вид: молекулы. Это соотношение имеет следующий вид:
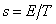 , , 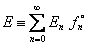 , , 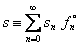 , , 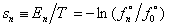 . .
Из приведенных утверждений следует главный вывод:
(а) число 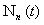 систем «молекула в систем «молекула в 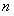 -ом квантовом состоянии + молекулярный газ» в ансамбле и полное число -ом квантовом состоянии + молекулярный газ» в ансамбле и полное число 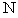 систем «молекула + молекулярный газ» в ансамбле не представляют собой чисел молекул в системе; систем «молекула + молекулярный газ» в ансамбле не представляют собой чисел молекул в системе;
(б) если энергия молекулы является случайной величиной, то функция 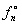 (квантовое каноническое распределение Гиббса) не зависит от числа молекул в системе. (квантовое каноническое распределение Гиббса) не зависит от числа молекул в системе.
Этот результат служит основой при анализе распределения Больцмана.
2. Анализ распределения Больцмана
Как известно, распределение Больцмана имеет следующий вид:
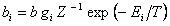 , ,
где 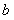 - полная плотность молекул (т.е. полное число молекул в единице объема); - полная плотность молекул (т.е. полное число молекул в единице объема); 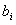 - плотность молекул в - плотность молекул в 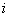 -ом квантовом состоянии (т.е. населенность -ом квантовом состоянии (т.е. населенность 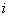 -го квантового уровня); -го квантового уровня); 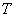 - температура; - температура; 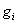 - кратность вырождения - кратность вырождения 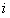 -го состояния; and -го состояния; and 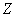 - статистическая сумма. С точки зрения теории вероятностей и квантового канонического распределения Гиббса, распределение Больцмана не свободно от возражений. Возражения состоят в следующем: - статистическая сумма. С точки зрения теории вероятностей и квантового канонического распределения Гиббса, распределение Больцмана не свободно от возражений. Возражения состоят в следующем:
(а) распределение Больцмана не является следствием (т.е. частным случаем) квантового канонического распределения Гиббса. Чтобы доказать это утверждение, следует предположить обратное: распределение Больцмана при некоторых условиях тождественно квантовому каноническому распределению Гиббса. Доказательство состоит в следующем. Разрешая функции Больцана и Гиббса относительно фактора 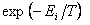 и подставляя полученные выражения соответственно в левую и правую части тождества и подставляя полученные выражения соответственно в левую и правую части тождества
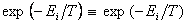 , ,
можно получить тождество
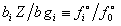 . .
Это тождество приводится к следующему виду:
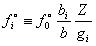 , т.е. , т.е. 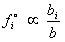 . .
Полученное выражение означает, что вероятность 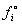 определяется отношением плотностей молекул, т.е. вероятность определяется отношением плотностей молекул, т.е. вероятность 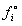 зависит от числа молекул в системе при любых услових. Но, с точки зрения квантового канонического распределения Гиббса, это противоречит определению вероятности. Следовательно, сделанное предположение не верно. Таким образом, распределение Больмана не является следствием (т.е. частным случаем) квантового распределения Гиббса; зависит от числа молекул в системе при любых услових. Но, с точки зрения квантового канонического распределения Гиббса, это противоречит определению вероятности. Следовательно, сделанное предположение не верно. Таким образом, распределение Больмана не является следствием (т.е. частным случаем) квантового распределения Гиббса;
(б) распределение Больцмана не основано на математической теории вероятностей, не является следствием математической теории вероятностей, потому что в больцманоской теории совокупность молекул газа рассматривается как статистический ансамбль. Больцманоская точка зрения приводит к некорректному определению вероятности, поскольку противоречит теории вероятностей. Действительно, с теоретико-вероятностной точки зрения, число систем «молекула в 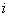 -ом квантовом состоянии + молекулярный газ» в ансамбле представляет собой число случаев осуществления события «молекула в -ом квантовом состоянии + молекулярный газ» в ансамбле представляет собой число случаев осуществления события «молекула в 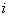 -ом квантовом состоянии». Поэтому вероятность есть предел отношения чисел случаев, а не чисел молекул. Это означает, что распределение Больцмана не представляет собой результата (следствия) теории вероятностей. -ом квантовом состоянии». Поэтому вероятность есть предел отношения чисел случаев, а не чисел молекул. Это означает, что распределение Больцмана не представляет собой результата (следствия) теории вероятностей.
Заключение
Таким образом, критический анализ распределения Больцмана на основе квантового канонического распределения Гиббса и теории вероятностей приводит к выводу, что распределение Больцмана не является следствием (частным случаем) ни квантового канонического распределения Гиббса, ни теории вероятностей. С этой точки зрения, распределение Больцмана не имеет ни физического, ни статистического смысла. Следовательно, понятия «распределение Больцмана» и «населенность уровня» должны быть упразднены. Теперь они могут быть упразднены, потому что распределение Больцмана уже сыграло свою роль «ложной гипотезы, оказавшей большую услугу» при построении теории лазера.
Как известно, «часто ложные гипотезы оказывали больше услуг, чем верные» (А. Пуанкаре). И распределение Больцмана не оказалось исключением: понятия «населенность квантового уровня» и «инверсия населенностей» легли в основу теории лазера, предложенной и опубликованной Чарльзом Таунсом и Артуром Шавловым (Charles Hard Townes and Arthur Leonard Schawlow) в журнале “Physical Review” (1958). С тех пор, «инверсия населенностей – необходимое условие генерации и усиления электромагнитных колебаний во всех устройствах квантовой электроники» (Физический энциклопедический словарь). Но сегодня, как показано в настоящей работе, это утверждение хотя и «выглядит убедительным, оказывается не обоснованным» (Р. Пайерлс). Поразительны не «успехи физических наук», а неуспехи, ошибки физических наук. «Кажется, что главная шутка, которую сыграл с нами неистощимый на загадки Создатель, пока совершенно не понята» (Эйнштейн).
Литература
[1] T.Z. Kalanov, “Modern analysis of the Boltzmann distribution”, Gallilean Electrodynamics (be published).
[2] Б.В. Гнеденко. «Курс теории вероятностей». М.: Наука, 1988.
[3] Л.З. Румшиский. «Элементы теории вероятностей». М.: Наука, 1966.
[4] T.Z. Kalanov, “The correct theoretical analysis of the foundations of classical thermodynamics”, Bull. of Pure and Applied Sciences, Vol. 26D, No 2 (2007), pp. 109-118 (www.bulletinpureappliedscience.com).
|