Темур Зикириллаевич Каланов
кандидат физико-математических наук,
старший научный сотрудник
Дом физических проблем, г. Ташкент, Узбекистан
t.z.kalanov@rambler.ru
Критический анализ оснований дифференциального и интегрального исчислений
Аннотация. Предлагается критический анализ стандартных оснований дифференциального и интегрального исчислений. Методическим базисом анализа является единство формальной логики и рациональной диалектики. Показывается, что стандартные основания дифференциального и интегрального исчислений базируются на логически и практически ошибочных понятиях «бесконечно малая (бесконечно умаляющаяся) величина», «производная», «производная как функция переменной величины» и, следовательно, представляют собой некорректный базис математики.
Ключевые слова: основания математики, философия математики
«Физика, во-первых, дает нам предчувствия решения; во-вторых, подсказывает нам ход рассуждений» (Анри Пуанкаре).
|
Введение
Как известно, формализм дифференциального и интегрального исчислений широко и успешно используется в естественных науках. Изложению современного состояния этого раздела математики посвящено много работ. Однако это не означает, что проблема обоснования дифференциального и интегрального исчислений полностью решена в 20-21 веках и теперь основания дифференциального и интегрального исчислений не нуждаются в формально-логическом анализе. В последнее время возникла необходимость критического анализа оснований дифференциального и интегрального исчислений в рамках корректного методологического базиса – единства формальной логики и рациональной диалектики.
Критический анализ невозможен без правдоподобных рассуждений. «Мы закрепляем свои математические знания доказательными рассуждениями, но подкрепляем свои предположения правдоподобными рассуждениями. Все новое, что мы узнаем о мире, связано с правдоподобными рассуждениями, являющимися единственным типом рассуждений, которым мы интересуемся в повседневных делах. Математика в процессе создания напоминает любые другие человеческие знания, находящиеся в процессе создания. Вы должны догадаться о математической теореме, прежде чем ее докажете; вы должны догадаться об идее доказательства, прежде чем проведете его в деталях. Результат творческой работы математика – доказательное рассуждение, доказательство; но доказательство открывается с помощью правдоподобно рассуждения, с помощью догадки. Доказательное рассуждение и правдоподобное рассуждение дополняют друг друга. Решение математической задачи также может внушаться природой; физика обеспечивает нас такими ключами. Математическая картина была бы слишком узкой без решения с помощью физической интерпретации» [1].
В настоящее время нет критических математических работ, выполненных в рамках корректного методологического базиса – единства формальной логики и рациональной диалектики. Цель данной работы – предложить критический анализ оснований дифференциального и интегрального исчислений, основанный на правдоподобном рассуждении в рамках методологического базиса – единства формальной логики и рациональной диалектики.
Правдоподобные основания дифференциального и интегрального исчислений
Дана непрерывная функция 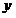 одного аргумента одного аргумента 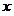 : :
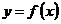 . .
1. Пусть аргумент 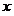 получает приращение получает приращение 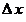 . Новое (наращенное) значение аргумента есть . Новое (наращенное) значение аргумента есть 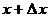 . Тогда величина функции . Тогда величина функции 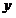 получит приращение получит приращение 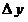 , и новым (наращенным) значением функции будет , и новым (наращенным) значением функции будет
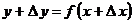 . .
Приращение 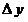 функции имеет вид: функции имеет вид:
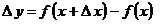 . .
2. Если приращение 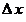 аргумента стремится к нулю (т.е. аргумента стремится к нулю (т.е. 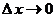 ), то ), то 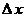 делается бесконечно малым (т.е. непрерывно умаляющимся). Предел этого стремления записывается следующим образом: делается бесконечно малым (т.е. непрерывно умаляющимся). Предел этого стремления записывается следующим образом:
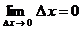 . .
3. Понятия «переменная величина 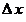 стремится к пределу стремится к пределу 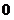 », «переменная величина », «переменная величина 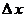 , стремящаяся к пределу , стремящаяся к пределу 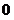 » и «процесс стремления переменной величины » и «процесс стремления переменной величины 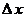 к пределу к пределу 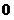 » не тождественны понятию «предел переменной величины » не тождественны понятию «предел переменной величины 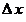 равен равен 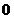 », т.е. выражение », т.е. выражение 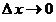 не тожественно выражению не тожественно выражению 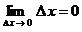 : :
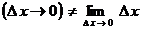 . .
4. Понятие «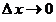 » кратко обозначается символом » кратко обозначается символом 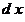 : :
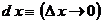 . .
«Переменная величина» 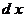 является бесконечно умаляющейся величиной и называется дифференциалом переменной величины является бесконечно умаляющейся величиной и называется дифференциалом переменной величины 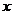 [2, 3]. Переменная величина [2, 3]. Переменная величина 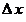 в выражении в выражении 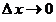 и «переменная величина» и «переменная величина» 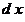 пробегают множество допустимых значений, не останавливаясь ни на одном из них. пробегают множество допустимых значений, не останавливаясь ни на одном из них.
5. Если 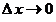 , то приращение , то приращение 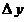 функции является бесконечно малым: функции является бесконечно малым: 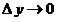 . Предел этого стремления записывается следующим образом: . Предел этого стремления записывается следующим образом:
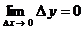
6. Понятия «переменная величина 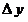 стремится к пределу стремится к пределу 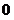 », «процесс стремления переменной величины », «процесс стремления переменной величины 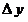 к пределу к пределу 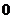 » и «переменная величина » и «переменная величина 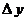 , стремящаяся к пределу , стремящаяся к пределу 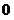 » не тождественны понятию «предел переменной величины » не тождественны понятию «предел переменной величины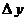 равен равен 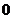 », т.е. выражение », т.е. выражение 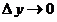 не тожественно выражению не тожественно выражению 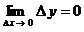 : :
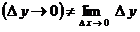 . .
7. Понятие «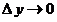 » кратко обозначается символом » кратко обозначается символом 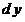 : :
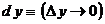 . .
«Переменная величина» 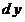 является бесконечно умаляющейся величиной и называется дифференциалом переменной величины является бесконечно умаляющейся величиной и называется дифференциалом переменной величины 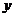 [2, 3]. Переменная величина [2, 3]. Переменная величина 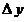 в выражении в выражении 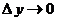 и «переменная величина» и «переменная величина» 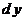 пробегают множество допустимых значений, не останавливаясь ни одном из них. пробегают множество допустимых значений, не останавливаясь ни одном из них.
8. Отношение приращений и предел этого отношения имеют вид:
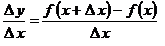 , ,
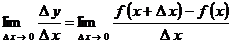
9. Отношение приращений
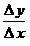
до перехода к пределу зависит от двух переменных величин: а) от начального значения 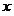 аргумента; б) от величины приращения аргумента; б) от величины приращения 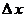 аргумента. Но предел этого отношения при аргумента. Но предел этого отношения при 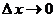 перестает уже зависеть от исчезающего перестает уже зависеть от исчезающего 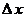 , потому что при отыскании указанного предела начальное значение , потому что при отыскании указанного предела начальное значение 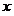 аргумента предполагается постоянной величиной (всякий предел переменной величины есть величина постоянная) [2, 3]. Поэтому предел аргумента предполагается постоянной величиной (всякий предел переменной величины есть величина постоянная) [2, 3]. Поэтому предел
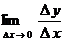 , ,
будучи величиной постоянной, может оказаться зависящим только от начального значения аргумента 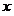 . Этот предел является выражением, содержащим только букву . Этот предел является выражением, содержащим только букву 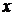 , и, следовательно, это есть некоторая новая функция , и, следовательно, это есть некоторая новая функция 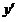 (или (или 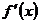 ) аргумента ) аргумента 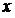 . .
10. Новая функция 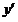 (или (или 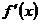 ) аргумента ) аргумента 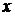 , произведенная данной функцией , произведенная данной функцией 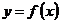 , называется производной функции от данной функции , называется производной функции от данной функции 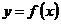 . Подчеркивая то обстоятельство, что эта новая функция произведена данной функцией . Подчеркивая то обстоятельство, что эта новая функция произведена данной функцией 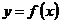 с помощью некоторого процесса, производную обозначают такими символами: с помощью некоторого процесса, производную обозначают такими символами: 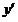 или или 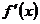 . .
11. Отношение дифференциалов
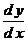
имеет следующий смысл:
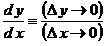 . .
Очевидно,
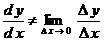
12. Если соотношение между 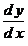 и и 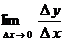 имеет вид имеет вид
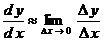 , т.е. , т.е. 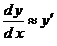 , ,
или форму строгого равенства [2, 3]
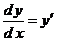 , т.е. , т.е. 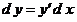 , ,
то это соотношение представляют собой постулат, основанный на интуиции и следующем частном предположении:
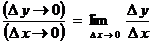
13. Прекращение процесса 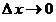 , , 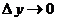 и возвращение от бесконечно малых (т.е. бесконечно умаляющихся) переменных величин и возвращение от бесконечно малых (т.е. бесконечно умаляющихся) переменных величин 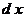 , , 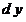 к конечным переменным величинам к конечным переменным величинам 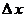 , , 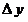 , не стремящимся к , не стремящимся к 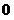 , осуществляется операцией интегрирования, обозначаемой символом интеграла , осуществляется операцией интегрирования, обозначаемой символом интеграла 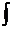 : :
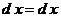 , , 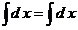 , , 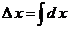 . . 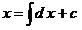 , где , где 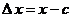 , , 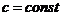 ; ;
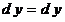 , , 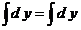 , , 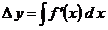 , , 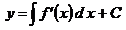 , где , где 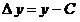 , , 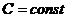 . .
Приведенные выше формулы удовлетворяют закону формальной логики – закону тождества, так как левая и правая части формул имеют один и тот же смысл, принадлежат одной и той же качественной определенности:
(бесконечно умаляющаяся величина)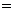 (бесконечно умаляющаяся величина) (бесконечно умаляющаяся величина)
и
(конечная величина)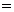 (конечная величина). (конечная величина).
Обсуждение
1. Главное различие между полученными формулами и стандартными (общепринятыми) формулами дифференциального исчисления состоит в том, что стандартные формулы [2, 3]
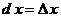 , , 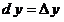
не удовлетворяют закону формальной логики – закону тождества, так как левая и правая части формул не имеют одного и того же смысла, не принадлежат одной и той же качественной определенности. Действительно, переменные величины 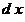 и и 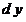 – это бесконечно малые (т.е. бесконечно умаляющиеся) величины, а переменные величины – это бесконечно малые (т.е. бесконечно умаляющиеся) величины, а переменные величины 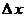 и и 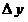 – конечные (т.е. не бесконечно умаляющиеся) величины. С точки зрения формальной логики (т.е. закона тождества), должно выполняться отношение тождества между величинами: – конечные (т.е. не бесконечно умаляющиеся) величины. С точки зрения формальной логики (т.е. закона тождества), должно выполняться отношение тождества между величинами:
(бесконечно умаляющаяся величина)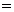 (бесконечно умаляющаяся величина) (бесконечно умаляющаяся величина)
и
(конечная величина)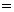 (конечная величина). (конечная величина).
Кроме того, согласно закону противоречия, бесконечно малые (т.е. бесконечно умаляющиеся) величины и конечные (не бесконечно умаляющиеся) величины должны быть связаны логическим отношением отрицания:
(бесконечно умаляющаяся величина)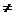 (не бесконечно умаляющаяся величина). (не бесконечно умаляющаяся величина).
Но стандартные математические соотношения
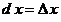 , , 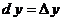
противоречат закону тожества и, следовательно, представляют собой логическую ошибку.
2. В классической механике использование определения производной приводит к логической ошибке. Действительно, пусть материальная точка 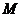 движется в положительном направлении оси движется в положительном направлении оси 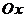 и характеризуется координатой и характеризуется координатой 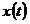 - непрерывной функцией времени - непрерывной функцией времени 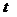 . Если . Если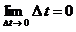 , то , то 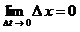 , т.е., в соответствии с практикой и формальной логикой, значение координаты не изменяется и, следовательно, движения нет (т.к. по определению, движение есть изменение вообще). Но, в противоречии с практикой и формальной логикой, дифференциальное исчисление и классическая механика содержат утверждение, что скорость , т.е., в соответствии с практикой и формальной логикой, значение координаты не изменяется и, следовательно, движения нет (т.к. по определению, движение есть изменение вообще). Но, в противоречии с практикой и формальной логикой, дифференциальное исчисление и классическая механика содержат утверждение, что скорость 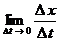 существует без движения. Тогда скорость существует без движения. Тогда скорость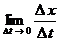 является не реальной (т.е. не физической) величиной, а фиктивной величиной. Поэтому использование нефизической (нереальной) величины (т.е. первой и второй производной функции) в классической механике является логической ошибкой. является не реальной (т.е. не физической) величиной, а фиктивной величиной. Поэтому использование нефизической (нереальной) величины (т.е. первой и второй производной функции) в классической механике является логической ошибкой.
3. Согласно формальной логике (т.е. закону тождества и закону противоречия), должны выполняться следующие логические отношения между величинами:
(реальная величина) 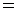 (реальная величина), (реальная величина),
(нереальная величина) 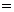 (нереальная величина), (нереальная величина),
(реальная величина) 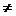 (нереальная величина). (нереальная величина).
Но
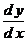
в соотношении
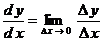
является нереальной величиной, математической фикцией. Следовательно, соотношение
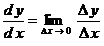
представляет собой логическую ошибку.
4. Бесконечно малая (бесконечно умаляющаяся) величина не может принимать численные значения. Действительно, если подставить, например, 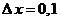 в соотношение в соотношение
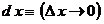 , ,
то получится бессмысленное соотношение:

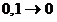 . .
Переменные величины 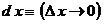 и и 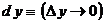 стремятся к нулю, не принимая ни одного численного значения. Но такое поведение переменных величин противоречит опыту. Следовательно, бесконечно малые величины стремятся к нулю, не принимая ни одного численного значения. Но такое поведение переменных величин противоречит опыту. Следовательно, бесконечно малые величины 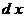 , , 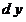 являются фиктивными величинами, и понятие «бесконечно малая величина» представляет собой логическую ошибку. являются фиктивными величинами, и понятие «бесконечно малая величина» представляет собой логическую ошибку.
5. Бесконечно малые величины (например, 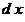 и и 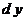 ) не имеют ни алгебраического смысла, ни геометрического смысла, т.к. эти величины не принимают численных значений и, следовательно, не имеют количественной меры. Это означает, что ) не имеют ни алгебраического смысла, ни геометрического смысла, т.к. эти величины не принимают численных значений и, следовательно, не имеют количественной меры. Это означает, что
величина 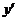 не является коэффициентом в соотношении не является коэффициентом в соотношении
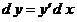 . .
Кроме того, с точки зрения формальной логики, выражения типа 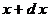 ошибочны, потому что ошибочны, потому что 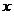 (т.е. конечная величина) и (т.е. конечная величина) и 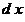 (т.е. бесконечно малая величина) имеют разный смысл, разную качественную определенность. Также, производная (т.е. бесконечно малая величина) имеют разный смысл, разную качественную определенность. Также, производная 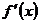 не имеет геометрического смысла. Действительно, если не имеет геометрического смысла. Действительно, если
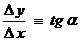 , ,
(где 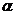 – угол наклона секущей линии к оси абсцисс), то положение секущей линии становится неопределенным при – угол наклона секущей линии к оси абсцисс), то положение секущей линии становится неопределенным при 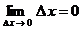 и и 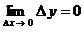 , потому что: (а) треугольник, образованный прямолинейными отрезками , потому что: (а) треугольник, образованный прямолинейными отрезками 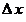 , , 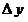 и секущей линией, вырождается (треугольник и угол и секущей линией, вырождается (треугольник и угол 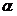 не существуют); (б) через одну точку не существуют); (б) через одну точку 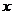 проходит множество прямых линий. Но одна точка проходит множество прямых линий. Но одна точка 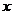 не определяет положения прямой линии. Следовательно, величина не определяет положения прямой линии. Следовательно, величина
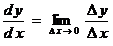
не определяет касательной линии.
6. В согласии с формальной логикой, справедливо следующее утверждение: если переменная величина 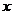 принимает численные значения принимает численные значения 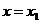 и и 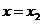 , то , то
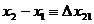 , , 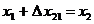 , ,
где 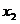 представляет собой результат операции сложения представляет собой результат операции сложения 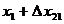 . Различие между переменными величинами . Различие между переменными величинами 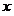 , , 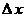 и их численными значениями выражается с помощью нижних индексов. Для того, чтобы перейти от операции сложения численных значений к операции сложения переменных величин и их численными значениями выражается с помощью нижних индексов. Для того, чтобы перейти от операции сложения численных значений к операции сложения переменных величин 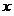 и и 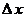 , следует удалить нижние индексы в числовых выражениях. Тогда получается следующее соотношение: , следует удалить нижние индексы в числовых выражениях. Тогда получается следующее соотношение: 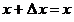 . Это соотношение согласуется с формулой . Это соотношение согласуется с формулой
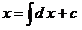 , , 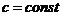
только при условии 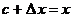 . При этом условии выражение . При этом условии выражение
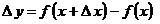
принимает корректный вид:
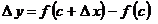 . .
Отсюда видно, что 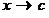 при при  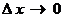 . В этом случае . В этом случае
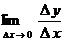
не содержит переменной величины 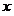 и зависит только от и зависит только от 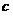 . Это означает, что дифференциальное исчисление является некорректной теорией, потому что формула для производной содержит переменную величину . Это означает, что дифференциальное исчисление является некорректной теорией, потому что формула для производной содержит переменную величину 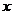 . .
Заключение
Таким образом, основания стандартных дифференциального и интегрального исчислений [2, 3] базируются на логически и практически ошибочных понятиях «бесконечно малая (бесконечно умаляющаяся) величина», «производная», «производная как функция переменной величины 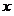 » и, следовательно, представляют собой некорректный базис математики. Поистине, стандартная «математика есть доктрина, в которой неизвестно, о чем мы говорим и верно ли то, что мы говорим» (Бертран Рассел). » и, следовательно, представляют собой некорректный базис математики. Поистине, стандартная «математика есть доктрина, в которой неизвестно, о чем мы говорим и верно ли то, что мы говорим» (Бертран Рассел).
Литература
[1] G. Polya. Mathematics and plausible reasoning. Princeton, 1954.
[2] В.И. Смирнов. Курс высшей математики. Т. 1. Москва, 1974.
[3] Н.Н. Лузин. Дифференциальное исчисление. Москва, 1952.
|