Москва. Апрель 1993 г.
Цифровой Танграмм от Корнеева
Историческая справка:
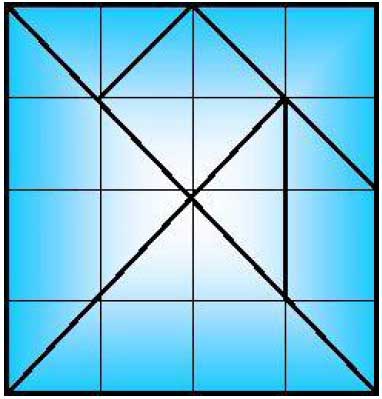 |
Танграмм – это известная всему миру игра, созданная на основе древних китайских головоломок.
По легенде, 4 тысячи лет назад у одного мужчины выпала из рук керамическая плитка и разбилась на 7 частей. Взволнованный, он посохом попытался её собрать. Но из вновь составленных частей каждый раз получал новые интересные изображения. Это занятие вскоре оказалось настолько захватывающим, головоломным, что составленный квадрат из семи геометрических фигур назвали Доской Мудрости.
Если разрезать квадрат, как показано на рисунке выше, то получится популярная китайская головоломка ТАНГРАМ, которую в Китае называют" чи тао ту", т.е. умственная головоломка из семи частей. Название "танграм" возникло в Европе вероятнее всего от слова" тань", что означает "китаец" и корня "грамма". У нас она сейчас распространена под названием "Пифагор" (? – А.К.).
Предлагаемая мною ниже новая игра – это существенно модифицированный вариант китайской игры. Она предназначена и для детей (для развития устного счёта, навыков геометрии, владения инструментом, развития абстрактного мышления, а также смекалки) и для взрослых, которые всерьёз занимаются исследованием чисел.
Итак, конечный механизм игры по-прежнему включает в себя процесс сложения фигурок сильно напоминающих фигурки Танграмм, однако имеются следующие отличия:
- Элементы для сложения танграмм – каждый раз разные и изготавливаются заново, с использованием бумаги, ножниц и линейки.
- Базовые элементы для игры – не фиксированы, а являются своеобразным продуктом преобразования исследуемых чисел, выбираемых по собственному усмотрению (или по подсказке взрослых).
- Для получения элементов необходимо производить вычисления, включающие в себя простое арифметическое сложение и специальное, нумерологическое (сложение) сокращение чисел (это детям объяснить не сложно).
Таких этапов математической подготовки будет всего 7.
После вычислений из плотного материала (с применением угольника и линейки) вырезаются 7 фигурок, у которых есть как лицевая, так и тыльная сторона, что может существенно разнообразить наборы собираемых фигурок.
Для ознакомления со способом получения элементов обратимся к моему способу обработки, который может быть назван способом «Квадратов»; Он излагается ниже.
Способ «Квадратов» для нового Танграмма
Способ применяется для получения (вычисления) элементов нового Танграмма на основе любых чисел, содержащих не менее 8 значащих цифр, и представляющих интерес для играющего (или исследователя).
Эти 4 цифры задуманного числа можно просто придумать.
А можно взять нужные цифры, например, из магического квадрата Дюрера (см. рис. Квадрата ниже), игнорируя при этом центральную ячейку (цифру 5).
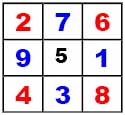 |
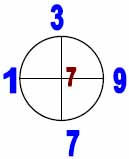
1. Рисуется вначале прямой (или косой) крест, на концах которого расставляют соответствующие цифры. Квадрат (точнее вспомогательный круг) помечается цифрой 1, как первый этап процедуры.
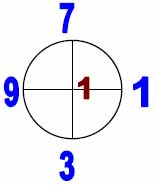 |
| Рис. 1 |
2. Второй этап (помечается цифрой 2).
Рисуется (для нашего случая) теперь уже косой крест (без указания цифр!), который мы таким образом подготавливаем для процедуры счёта.
На концах косых крестов проставляем рассчитанные (по правилу нумерологического сокращения) суммы двух цифр, которые «охватывают» данное направление косого креста (на прямом кресте).
Пример расчёта:
Левый верхний угол косого креста. = 7, так как соответствующий луч «охвачен» цифрами 9 и 7, а поэтому мы должны проставить здесь сумму: {9+7} = {16} — (1+6) = 7.
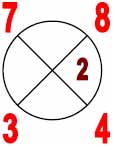 |
| Рис. 2 |
В фигурных скобках { } дана арифметическая сумма из цифр, взятых из Рис.1 /левая и верхняя цифры/;
3. Следующая операция – нумерологическое сложение (сокращение) предыдущего результата.
Мы имеем число {16}, нумерологическое сокращение которого означает всего лишь … сложение цифр, составляющих это число до тех пор, пока не получится одна цифра.
В нашем случае это – 1 + 6 = 7.
Именно эту (первую) цифру «7» мы и проставим в левом верхнем углу косого креста.
Правый нижний угол косого креста (для закрепления и усвоения способа).
Здесь необходимая цифра вычисляется из сложения правой и нижней цифр иза рисунка прямого креста (Рис.1), т.е. из цифр 1 и 3.
Таким образом, (1+3) = 4. Именно этот результат мы поставим в правый нижний угол косого креста.
Аналогично мы будем поступать с каждой цифрой каждого креста (прямого или косого), пока не получим новый (косой) крест с полной оцифровкой (см. Рис.2).
Можно было бы продолжить преобразования крестов ещё 7 раз, но при этом мы убедимся в странной закономерности преобразования данного вида, а именно в том, что конечный (7- й) крест будет содержать те же цифры, что и начальный, но в только в полном зеркальном отображении.
Для нас возвращение к точной исходной процедуре - это излишнее, так как уже говорилось, что получаемые элементы после их изготовления можно просто перевернуть другой стороной вверх.
Итак, продолжим наши вычисления «крестов» для получения данных об элементах нового Танграмма..
4. Снова берём прямой крест и проводится вся уже описанная выше процедура переоцифровки лучей. На этом этапе получим снова прямой крест, но с другими цифрами на концах (см. рис.3).
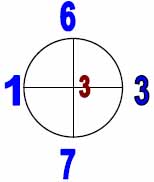 |
| Рис. 3 |
5. Далее процедура повторяется (РОВНО 7 РАЗ), после чего мы получим исходные данные для изготовления элементов триграмм, как уже отмечалось - в ПОЛНО - ЗЕРКАЛЬНОМ виде, где левое и правое, верх и низ – меняются местами.
6. Итак, мы получили в конце концов 7 разных «крестов», а точнее – те самые необходимые данные об элементах новых Танграмм. Ъ
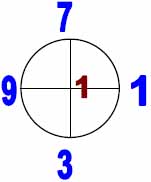
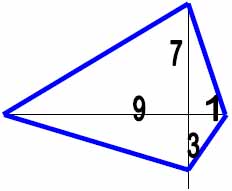
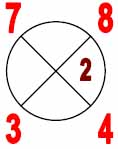
Посмотрим специальную табличку с кругами и крестами отображающими наши элементы.
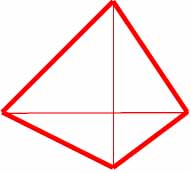
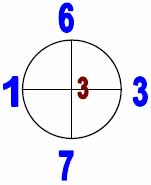
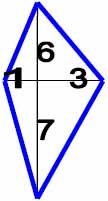
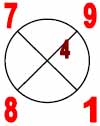
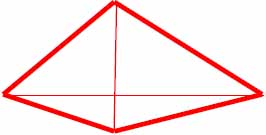
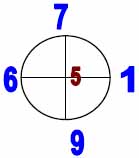
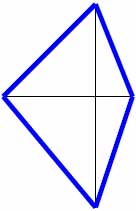
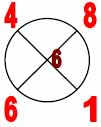
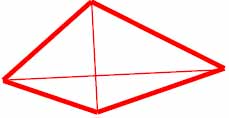
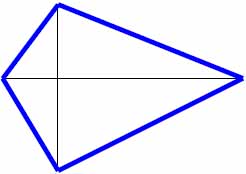
Таблица базовых элементов.
| Расчётные кресты (в кругах) | Элементы нового триграмма |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
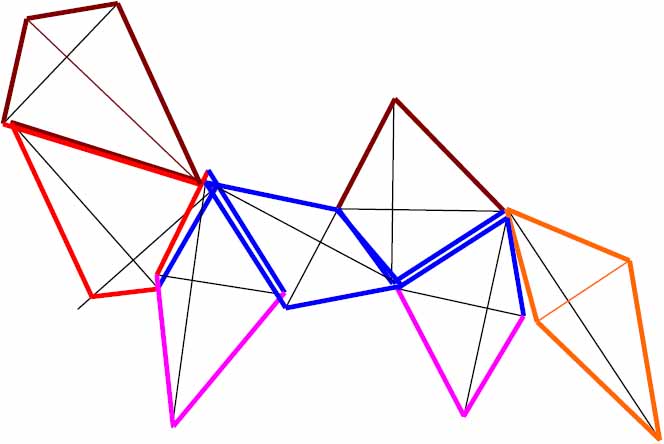
А теперь – приступайте к сборке картинок из элементов этой игры – нового Танграмма.
Вот и первый пример такой картинки: Дерзайте дальше сами!
 |