Исследование «союзных» группировок цифр в числах (Исследования изонумов)

Каждое трёхзначное число с помощью парных группировок цифр внутри этого числа можно представить набором других чисел; Общим свойством у всех них будет одинаковая нумерологическая сумма, а поэтому такие числа можно назвать «ИзоНумами».

Изонумы можно также выявить и записать и для зеркального (к исходному) числа. Тогда у нас будет полная группа охвата всех вариантов порождения новых чисел с помощью данной цифровой процедуры (манипуляции группирования).

После этого представляет интерес исследование всех этих чисел на предмет выявления внутренних закономерностей в их взаимоотношениях.

Возьмём произвольное трёхзначное число = 765 и «размножим» его (это - рабочая терминология – А.К.) для получения «изонумов». Суть используемой для этого группировки цифр числа – попарное их объёдинение внутри числа с вычислением как промежуточных нумерологических форм, так и конечных нумерологических сумм (корней).

ИТАК:

Однако, скрытые числа (прямых и обратных групп изонумов) связаны между собой:ибо 85/17 = 5, а потому соотношения для зеркальных изонумов можно привести в математическое соответствие с соотношениями для прямых изонумов.

Таким образом, число 85 = 765*15/135 = 765*5/45 – может выступать, как общее «скрытое, непроявленное число», характерное для специфической операции по получению «изонумов».

Итого, все (прямые и зеркальные) изонумы - числа связаны соотношениями:

765*79 /711= 765*9/81 = 765*8/72 = 765*2/18 = 765*15/135 = 765*5/45 = 85

Наборы «чисел – изонумов» таковы: 765; 711; 135; 81; 72; 45; 18 __567; 513; 117; 63: 54;

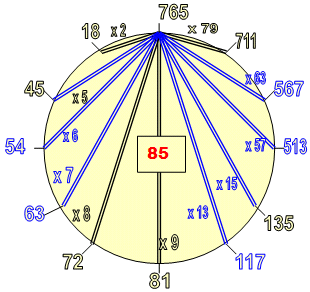
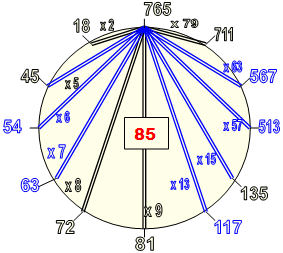
Общую картину взаимосвязи чисел - изонумов с исходным числом даёт Лимб-12, на котором исходное число (765) показано вверху лимба, а двойными линиями оно соединено с остальными числами, что подразумевает разные делители.

Рядом с линиями проставлены разные числа-множители, на которые умножается частное от деления, Во всех ситуациях получается общий результат = 85 (некое характеристическое число при операции по получению чисел - изонумов).

Возникает вопрос № 1: «А откуда взялось это число = 85 и нельзя ли его определять сразу (по отношению к исходному числу)?

Прежде всего, заметим, что 765: 85 = 9 (!)

В то же время можно увидеть, что частные от деления всех изонумов на вычисленную выше девятку (число – 9) дают нам соответственные множители, указанные на лимбе-12:

Это означает (по крайней мере для изонумов с «весом» равным = [9]) возможность:

1. Определить характеристические числа всех изонумов: по образцу - 765: 9 = 85 (!).
2. Определить множители связей: «изонум Х»:9 = множитель Х?

Вопрос №2: «Есть ли способы определения связей всех чисел – изонумов для данного исходного числа»?

Мы установили (вычислили) для данного исходного числа = 765 набор из 11 изонумов с их множителями (по убыванию значений изонумов):

Рассчитаем теперь суммы всех изонумов (строчками), последовательно вычитая из этой суммы по одному изонуму (начиная с наибольшего). Назовём результаты расчётов предельными суммами разных рангов: ПС₀, ПС₁, ПС₂ и т.д.

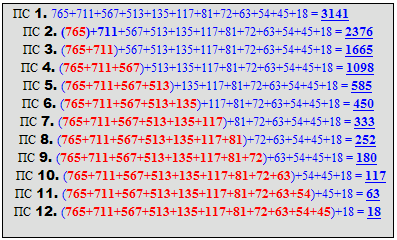Теперь построим таблицы, где найдём пропорции для этих чисел (ПС_Х), которые будут включать в себя и все ранее найденные множители (85, 79, 63, 57, 15, 13, 9, 8, 7, 6, 5, 2,).

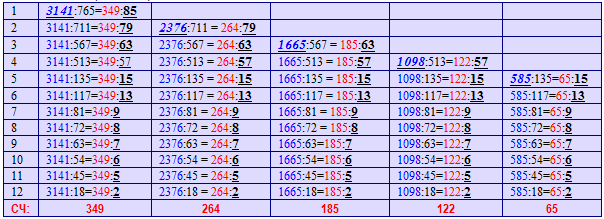
Таблица №1(начало)

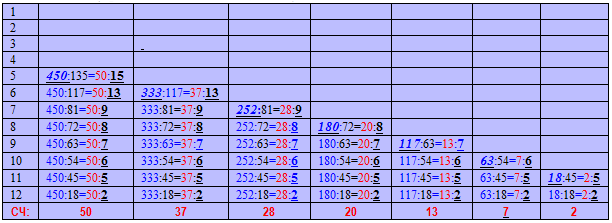
Таблица №2(продолжение таблицы №1)

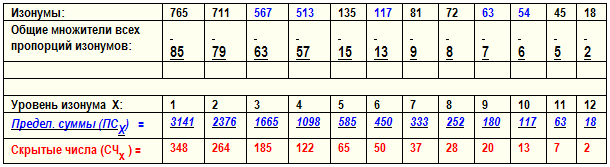
Обозначения:

- Косые, подчёркнутые числа, например, 450 – это «предельная сумма» (ПС₅) изонумов на 5 уровне;

- Числа без выделения (… 135, 117, 81…) – изонумы;

- Подчёркнутые числа (…15, 13, 9, 8, …) – множители пропорций для пар изонумов, например, 765 и 165 имеют множитель = 15;

- Красные числа (… 50, 37, 28,20…) – это «скрытые числа» (СЧ) группы «чисел – изонумов», характеризующих полную взаимосвязь всех изонумов внутри одного исходного числа.

Из таблиц (№1 и №2) можно видеть, что все изонумы закономерно подчинены строгим пропорциям, в которых участвуют (кроме самих чисел – изонумов) найденные с помощью лимба 12 числа-множители, а также – уже целый набор т.н. «скрытых чисел (СЧ)», которые также участвуют в тех же пропорциях.

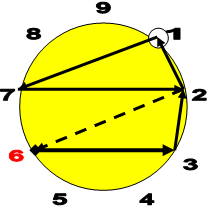
Последовательность скрытых чисел для изонумов прямого отображения (СЧПх) такова:

348, 264, 65, 37, 28, 7, 2 --- Сделаем нумерологическое сокращение: 6, 3, 2, 1, 1, 7, 2

Отобразим ряд на лимбе-9 (Рис 2):

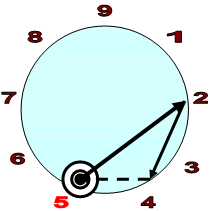
А последовательность изонумов зеркального отображения (СЧЗх) имеет вид:

185, 122, 50, 20, 13 --- Сделаем нумерологическое сокращение: 5, 5, 5, 2, 4

Отобразим ряд на лимбе-9 (Рис 3):

Прямые изонумы: 6, 3, 2, 1, 1, 7, 2	Зеркальные изонумы: 5, 5, 5, 2, 4

Из обзора лимбов-9 очевидно, что скрытые числа (СЧП и СЧЗ), относящиеся как к прямым, так и зеркальным изонумам, имеют строгие формы отображения своих форм в нумерологических образах, которые делают их наглядными, т.е вскрывают закономерный характер внутренней числовой структуры их отображающей.

Поэтому минимальные выводы, которые можно сделать, состоят в следующем:

1. Манипуляция (процедура, операция) по получению из исходного, трёхзначного числа - новых чисел (попарной группировкой цифр, но без перестановок цифр) порождает специфичные ряды чисел.
2. Аналогичный ряд новых чисел порождает та же манипуляция при её применении к зеркальному отражению исходного числа.
3. Полученные числа - изонумы имеют одну и ту же нумерологическую сумму и потому названы «изонумами».
4. Соотношения (пропорции) между изонумами выявляют скрытые характеристические числа, отражающие взаимоотношения между всеми изонумами, которые проявляются, как некие не явные числа (множители) к пропорциям изонумов.
5. Скрытые числа прямых и зеркальных изонумов после нумерологического сокращения и отображения на лимбах показывают две группы закономерных соотношений в виде разных траекторий рядов скрытых чисел на лимбах-9. Оба вида траекторий достаточно симметричны.
6. Вычисления пропорциональных связей между числами-изонумами выявило тот факт, что во всех случаях отношений любых пар изонумов в вычислениях присутствует один и тот же набор множителей этих пропорций.
7. Отношения изонумов и множителей выражаются только через целые числа и дают также целочисленные пропорции.
8. Формула для вычисления первичных множителей набора едина: Изонум X : [Изонум X] = Mx, где запись Изонум X означает числовое изображение одного (Х) из полученных изонумов.
9. [Изонум X] – результат нумерологического сокращения данного изонума, а Мх – вычисляемый множитель для первого уровня, который задан позицией соответствующего изонума (в порядке убывания их величины).
10. Самый первый уровень задаёт исходное число, а самый последний – наименьший из изонумов. Соответствующий этому уровню множитель участвует во всех пропорциях (отношениях любых изонумов между собой), а исходное число – только в попарных отношениях исходного числа с набором вычисленных изонумов.
11. Скрытые числа – это числа, которые выявляются после вычисления пропорций вида: 3141:765=349:85. В этой конкретной формуле 765 – исходное число (а может быть и один из изонумов); число 3141 – общая сумма всех изонумов и исходного числа; число 349 – константа для ряда, включающего все изонумы и исходное число (путём деления 3141 : 9 = 349); И, наконец, число 85, которое определяется из исходной пропорции (85 = [765*349] : 3141)и определяется как один из постоянных множителей данного ряда изонумов.
12. Возможна и другая запись: 3141 * 85 = 349*765, которая определяет, что знание исследуемого изонума (или исходного числа, как дано в примере) и константы конкретного ряда изонумов позволяет вычислить первый (и последующие) множители для этого ряда.

Практическая и теоретическая польза данного исследования.

1. Насколько известно автору, в математике такого рода манипуляции с числом ещё не исследовались и взаимоотношения получаемых в результате чисел также не изучались.
2. Вскрытая закономерность общих пропорций чисел, порождаемых данной операцией, и различие чисел, производных от прямой записи либо от зеркальной записи исходного числа, – также не рассматривались.
3. Не было известно, что совокупности ряда производных чисел, порождаемых данной манипуляцией, могут иметь ряд соответствующих констант, связанных с длиною, а точнее с суммой членов этого ряда.
4. Не было известно, что пропорции отношений всех порождаемых новых чисел, названных автором «изонумами», имеют общий для всех набор коэффициентов (множителей).
5. Эти множители позволяют связать между собой любой конкретный изонум, сумму ряда изонумов, начинающегося с данного изонума, константу ряда изонумов и конкретный множитель.
6. Практическая польза данного исследования состоит в том, что оно, будучи связано с самым трудным разделом математики – с арифметикой, расширяет наши представления о взаимоотношениях и закономерностях в сфере чисел, а также предоставляет исследователям новый подход и новые инструменты для изучения.
7. Предложенным автором способом можно исследовать числа, которые имеют (принципиально) любую размерность. Однако, для выполнения подобных вычислений, целесообразно написать специальную программу расчёта и отображения данных (как промежуточных, так и конечных).