Хлебниковская константа 317 и её родственники
В данной статье представлен авторский метод исследования чисел, который я предлагаю использовать, в частности, для изучения Хлебниковских «чисел – констант», таких как - «317», «365» и других.
Кроме того, здесь присутствует ещё один метод исследования, в котором «изюминкой» является использование простых дробей.
Этими методами я хотел бы вооружить исследователей числовых закономерностей теории Времени В. Хлебникова, да и просто исследователей тайн чисел.
Как писал сам Велимир Хлебников, это надо для того, чтобы … «удалось изыскать лад судеб, необходимый нам для переноса человечества на ладонь нашей мысли, на очередную ступень бытия. Ведь он движется, этот странник столетий. … чтобы люди имели …предвидение будущего не с пеной на устах, как у древних пророков, а при помощи холодного умственного расчета.
Излагаю по порядку.
Сущность метода заключается в следующих шагах и действиях:
Шаг 1. Выбираем исследуемое число и устанавливаем все его изоморфнве образы (далее – изоморфы), т.е. пишем все комбинации с перестановками цифр, имеющимися в данном числе. Получаем исходный набор чисел для дальнейших действий.
Шаг 2. Вычисляем нумерологический корень исходного числа (он будет одинаков и для чисел - изоморфов). Фиксируем его.
Шаг 3. Каждое из полученных в наборе чисел делим на число 11, что эзотерически означает сопоставление этого числа с Абсолютом. (Этим мы как бы устраеваем исследуемому числу «очную ставку» с самим Абсолютом, которая должна «высветить» всю подноготную этого числа). Для больших чисел полезно брать в качестве «делителя» не «11», а число «111», соответствующее Вселенной.
Шаг 4. Полученные десятичные дроби (используем калькулятор) НЕОБХОДИМО выразить (преобразовать) в виде ПРОСТЫХ ДРОБЕЙ. Это очень важно, поскольку именно (и только!) простые дроби наилучшим образом выявляют скрытых участников процессов взаимодействия между числами.
Шаг 5. Числа – изоморфы (в виде целых и простых дробных частей) располагаем на Лимбе такой же кратности, что и число изоморфов. Если для исходного 3-х значного числа мы получаем всего 6 изоморфов, то и лимб для их отображения будет иметь всего 6 точек на окружности (Лимб-6)
Шаг 6. Методом подбора и предварительных расчётов расставляем числа-изоморфы на Лимбе-6 так, чтобы добиться симметричного числового баланса между числами и относительно оси общей симметрии
Шаг 7. Рисуем окончательную картинку Лимба-6 с расставленными на его «делениях» числами и начинаем анализировать эту картинку, чтобы делать далеко идущие выводы J….
В качестве ОБЪЕКТА мы будем исследовать число, состоящее из цифр 1,3,7 – за которым разные исследователи усматривают и константу Велимира Хлебникова (317), «Константу тонкой структуры Вселенной» (1 / 137), число Смерти (137), число из пушкинской «Пиковой дамы» (371) - Тройку, Семёрку и Туза, и многое другое.
Вот мы и посмотрим на внутреннее содержание числа, состоящего из цифр 1, 3, 7, через призму нового метода.
Итак, указанные выше цифры (в составе числа – 137) имеют нумерологический корень = 1+3+7 = {11} --- [2];
Число 137 имеет соответствующие изоморфы (модификации с перестановками цифр):
137, 173, 317, 371, 713, 731
Нарисуем таблицу, в которой будет удобно отображать дальнейшие результаты.
Таблица 1.
https://xsp.ru/pub/pub00375/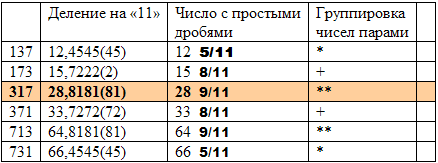 |
После группировки чисел по парам получим 3 главные пары чисел:
(137 – 173), (173 – 371), (317 – 713);
Общая сумма всех пар чисел: 310 + 544 + 1030 = 1884 –- {21} –- [3];
Установлено!
Баланс сумм этих пар чисел (левый и правый) выполняется только в таком раскладе:
«Левые»: 137 + 371 + 713 = 1221;
«Правые»: 731 + 317 + 173 = 1221;
Обратим внимание и на то, что: 1221 : 11 = 111 (!) – число Вселенной.
Уточнение баланса позволяет перейти к построениям на Лимбе-6.
Здесь возможны несколько вариантов расстановки чисел на лимбе:
По принципу вхождения в левые или правые (см. выше)
По принципу зеркального отображения цифр в парах чисел
По принципу «большее число – напротив меньшего»
По принципу возрастания (уменьшения) величины числа
Другие принципы различения и сортировки чисел
Вот - пример расположение по принципу баланса правых и левых:
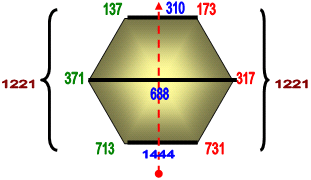 |
| Рис. 1 |
А это (ниже) - пример оцифровки лимба числами по принципу зеркальности:
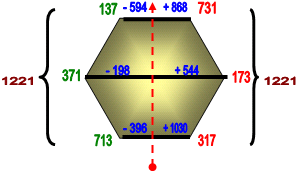 |
| Рис. 2 |
Теперь я приведу выведенную мной эмпирическую формулу представления для чисел – изоморфов. Согласно этой формуле для числа 137 можно записать следующее соотношение:
(731 – 137) = (713 – 317) + (371 – 173) = > (594) = (396) + (198) [1]
А для числа 317 - аналогичную формулу [2]:
(713 – 317) = (731-137) – (371) – (173) [2]
Формула [1] позволяет нам произвести сбалансированную оцифровку лимба - 6.
Как можно увидеть (Рис.3) – осуществлена группировка чисел попарно и по принципу их зеркальности.
Остановимся на одном из вариантов более детально. Ниже дана такая раскладка, когда связи между числами на лимбе показаны в виде разности значений пар чисел
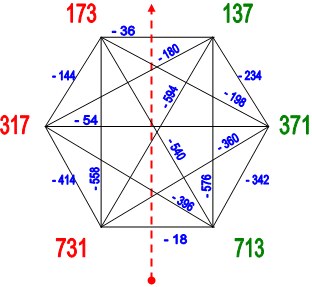 |
| Рис. 3 |
А в другом варианте (см. Рис. 4) все числа и величины сумм пар тех же чисел дополнительно разделены на число «11» и представлены в виде целых чисел с простой дробью.
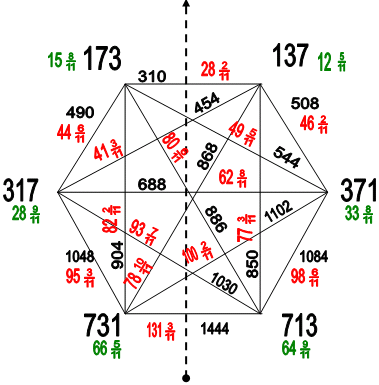 |
| Рис. 4 |
И, наконец, опираясь на обнаруженное свойство равенства одной половины чисел – изоморфов другой половине, можно построть новый лимб, где все тройки чисел геометрически объёдинены в треугольники, имеющие противоположную ориентацию вершин.
При этом можно прибегнуть к маленькой нумерологической хитрости, которую я называю:
НЕПОЛНОЕ НУМЕРОЛОГИЧЕСКОЕ СОКРАЩЕНИЕ.
Суть его в том, чтобы представить числа (из исследуемого набора) в другой, иной форме:
Конкретно: 137 à (13)7;
317 –> (31)7;
371 –> (37)1;
731 –> (73)1;
713 –> (71)3;
173 –> (17)3;
Цифры в скобках сложим опять-таки нумерологически и получим новые соответствия между исходными числами и итоговыми, синтезированными:
137 –> «47»;
317 –> «47»;
371 –> «101»;
731 –> «101»:
713 –> «83»;
173 –> «83»;
Теперь, благодаря хитрому приёму мы получаем возможность использовать и ставить этот хитрый индекс «Х» между теми числами-изоморфами, которые его порождают.
После этого можно заметить, глядя на рисунок, что незаполненные места можно заполнить соответствующими индексами «Х», если объединять уже не первые цифры чисел, а последние две их цифры.
Этими новыми индексами «Х» мы и дополним Лимб с оцифровкой, после чего снова вычислим нумерологические корни, но уже «чисел – индексов».
В итоге получим вот такую картину:
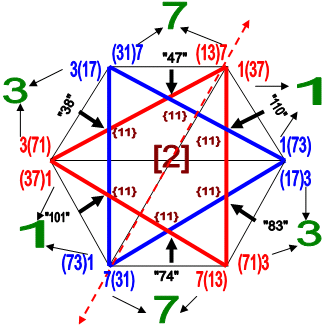 |
| Рис. 5 |
По этой картинке можно убедиться, что индивидуальная оцифровка лимба числами (из набора «чисел – изоморфов») даёт нам новую информацию и позволяет выявлять – с какими числами связаны исследуемые числа, а значит – и исходное Число.
Абрис соотношений чисел на Рис.5 отличается исключительной сбалансированностью и симметрией, а нумерологические «хитрые» индексы позволили выявить неслучайность этой сбалансированности и, значит, применённой данной оцифровки. Что мы и добивались.
Выявление правильной оцифровки – один из важнейших моментов такого рода исследований чисел и поэтому следует уделять этому большое внимание, точнее работе по построению лимбов такого рода методами.
А теперь составим сводную таблицу расчётных данных.
Таблица 2.
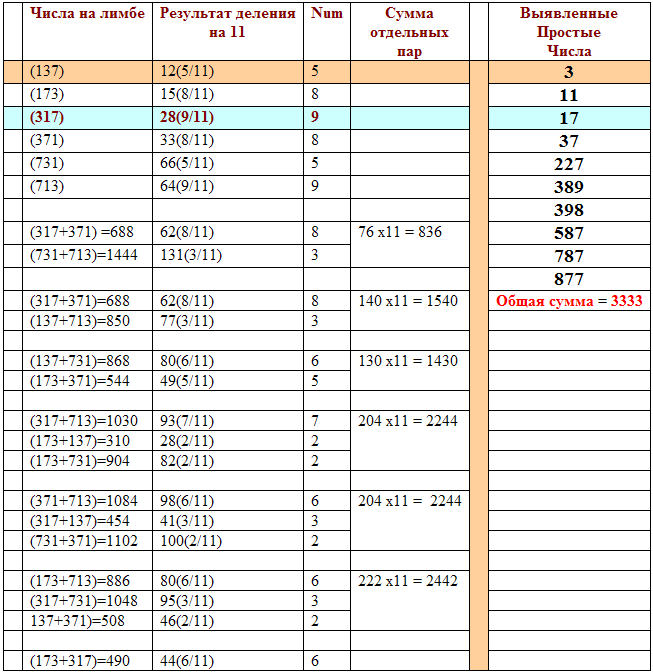 |
Посмотрим теперь на то, что НОВОГО, ранее скрытого, мы можем получить из наших картинок и подсчётов.
Нетрудно видеть, что нами собран неплохой «урожай»…
Периметр лимба: (137+173+317+371+713+731) = 2442 = 37 х 66
Обе половины Лимба равны 1221 = 37 х 3 х 11. (3, 11, 37 – простые числа!)
Суммы параллельных пар чисел – РАВНЫ между собой:
(310+688+1444) = (508+886+1048) = (490+868+1084) = 2442
Суммы разниц пар чисел (по периметру): (342+18+414+36+234) = 1188, а если разделить это число на 11, то получим – 1188: 11 = 108! (одна из общеизвестных констант).
Прямоугольники, выделяемые в лимбе включают в себя ПРОСТЫЕ числа:
310+850+1444+904 = 3508 = 4х 877; (877 – простое число!)
508+1102+1048+454 = 3112 = 8х 398; (398 – простое число!)
490+544+1084+1030 = 3148 = 4х 787; (787 – простое число!)
Сумма сумм «прямоугольников – 3508+3112+3148 = 9768 = 264 х 37 = 24 х 11 х 37
Большие треугольники в Лимбе-6:
454+850+1030 = 2334 = 6х 389 (389 – простое число!)
904+544+1102 = 2550 = 255х10 =150х 17 (17 – простое число!)
Сумма больших треугольников (2334+2550) = 4884, т.е. равна 2-м суммам периметра.
Малые («равнобедренные») треугольники по периметру Лимба - 6:
310+508+544 = 1362 = 6 х 227 (227 – простое число!)
508+1084+850 = 2442 = 222х11 = 37х11х6
1084+1444+1102 = 3630 = 330х11 (11 – простое число!)
1444+1048+1030 = 3522 = 6х 587 (587 – простое число!)
1048+490+904 = 2442 = 222х11
490+310+454 = 1254 = 11х114
Суммы противолежащих, параллельных отрезков на лимбе:
310+1444 = 1754 = 2х 877 (877 – простое число!)
508+1048 = 1556 = 3х 389 (389 – простое число!)
490+1084 = 1574 = 2х 787 (787 – простое число!)
Наиболее правильная оцифровка соответствует Рисунку 5 (ось симметрии – 137 – 731).
Выявлено большое количество Простых Чисел, с которымине вполне ведомыми пока методами (к сожалению), но, безусловно, связано ИСХОДНОЕ число 137,
Само исходное число 137 – тоже, кстати, ПРОСТОЕ.
Общая сумма всех выявленных в исследовании простых чисел (см. таблицу) равна числу 3333 (!??).
Данное исследование, кроме прочего, показало также и эффективность нового способа «Неполного нумерологического сокращения» для изучения нахождения правильной оцифровки лимба с изоморфами исследуемого числа.
Дальнейшие исследования можно вести используя в расчётах найденные соотношения и простые числа и, анализируя пропорции между ними, исходным числом (137) и другими числами - изоморфами.
Заключение:
Все НОВЫЕ числа и соотношения, которые были здесь получены, тесно связаны как с исходным числом, так и с его изоморфами.
Во всех дальнейших расчётах они могут служить твёрдыми ориентирами для формулировки (вывода) закономерностей и связей исследуемого числа с иными числами, могут помочь при обнаружении констант в уравнениях, о которых (без этого метода) догадаться чрезвычайно трудно.
Следует учитывать, что традиционные, обычные «облики чисел» свою внутреннюю структуру (сами по себе!) никогда не раскрывают, ибо подразумевается, что числа, как бы начисто лишены любой качественной определённости.
Сделать видимой внутреннюю структуру возможно только посредством разработки и применения необычных, нетрадиционных правил и методов манипуляций с числами, подобных тем, что рассмотрены в данной статье.