Как Пифагор помогает в клонировании живого
| |
Прошла ли золотая пора открытий в сфере арифметики? Всё уже изобретено и открыто? Академик В.И. Вернадский, основатель науки о ноосфере, говаривал по этому поводу:
«Не верьте в чудеса! Не верьте!
Смело опирайтесь на них в своих исследованиях…» |
В обычной практике исследования физических объектов мы обычно делаем следующее:
1. Наблюдаем объект в его естественном движении и подмечаем особенности этого движения.
2. Сопоставляем этот объект (и его движение) с другим подобным (или не подобным) объектом.
3. Изучаем внешние проявления объекта в среде подобных (или имеющихся) объектов, а также характерные взаимодействия исследуемого объекта
4. Исследуем внешние характеристики и объекты.
5. Исследуем строение объекта (его части, элементы, связи элементов и их иерархию, функции).
6. Изучаем функциональное предназначение объекта в целом и соответствующие характеристики (количественные и качественные)
7. Изучаем внутренние движения элементов объекта, специфику и особенности этих движений.
8. Пытаемся приспособить полученные знания об объекте к вопросам своей жизнедеятельности.
Как известно, арифметические действия с цифрами и числами это некие манипуляции, выполнение которых обеспечивает желаемый результат, на который эти действия «настроены».
Здесь мы будем разбираться с такого рода манипуляциями, как таковыми.
Но сначала используем, сказанное выше, о физических объектах применительно к числам и цифрам.
Итак, п. 1: Наблюдаем объект в его естественном движении и подмечаем особенности этого движения.
Перед этим отметим одно важное обстоятельство. Для того, чтобы можно было сопоставлять между собой данные о движениях разных объектов, часто используют метод, при котором перемещения объёкта фиксируют не за единицу времени а по принципу - «сколько раз объект отложится на траектории своего движения со старта до финиша». Это позволяет, например, сравнить движения автомобиля и майского жука.
Теперь возьмём для мысленного эксперимента двух жуков: майского и июньского, а также шершня. Как известно, майский жук имеет размеры ~ в 2 раза больше, чем июньский. Примем размер июньского жука равными = 1см, а майского = 2 см. Третьим, (контрольным объектом) будет шершень с длиной туловища L = 3см.
Теперь составим таблицу движений этих насекомых по указанному выше принципу. Фазой движения мы будем называть некий промежуток времени, за который каждое из насекомых сможет переместиться вперёд на величину своего корпуса.
Количество регистрируемых фаз движения можно сделать сколь угодно большим. Но, мы ограничимся примерно 20–ю фазами.
В строчках таблицы № 1 (на соответствующих фазах) мы будем отмечать длину пути, которую пройдут наши объекты (по любым своим траекториям) к цели.
Теперь произведём ещё одну манипуляцию с данными в таблице №1 и осуществим так называемое «нумерологическое сокращение» числовых данных, отображающих путь, проделанный нашими насекомыми. Эти вычисления мы, естественно, отобразим в таблице № 1.
Посмотрим в таблицу и… увидим что-то не совсем обычное!
|
Таблица № 1.
|
Июньский жук
L=1см |
Майский жук
L=2см |
Шершень
L=3см |
№_Фазы
движения |
Длины пройденного пути для всех насекомых
(см. в соответствующих столбцах ниже) |
| 1 |
1 |
2 |
3 |
| 2 |
2 |
4 |
6 |
| 3 |
3 |
6 |
9 |
| 4 |
4 |
8 |
12=(1+2)=3 |
| 5 |
5 |
10=(1+0)=1 |
15=(1+5)=6 |
| 6 |
6 |
12=(1+2)=3 |
18=(1+8)=9 |
| 7 |
7 |
14=(1+4)=5 |
21=(2+1)=3 |
| 8 |
8 |
16=(1+6)=7 |
24=(2+4)=6 |
| 9 |
9 |
18=(1+8)=9 |
27=(2+7)=9 |
| 10 |
10=(1+0)=1 |
20=(2+0)=2 |
30=(3+0)=3 |
| 11 |
11=(1+1)=2 |
22=(2+2)=4 |
33=(3+3)=6 |
| 12 |
12=(1+2)=3 |
24=(2+4)=6 |
36=(3+6)=9 |
| 13 |
13=(1+3)=4 |
26=(2+6)=8 |
39=(3+9)=12=(1+2)=3 |
| 14 |
14=(1+4)=5 |
28=(2+8)=1 |
42=(4+2)=6 |
| 15 |
15=(1+5)=6 |
30=(3+0)=3 |
45=(4+5)=9 |
| 16 |
16=(1+6)=7 |
32=(3+2)=5 |
48=(4+8)=12 =(1+2)=3 |
| 17 |
17=(1+7)=8 |
34=(3+4)=6 |
51=(5+1)=6 |
| 18 |
18=(1+8)=9 |
36=(3+6)=8 |
54=(5+4)=9 |
| 19 |
19=(1+9)=10=(1+0)=1 |
38=(3+8)=1 |
57=(5+7)=12=(1+2)=3 |
| 20 |
20=(2+0)=2 |
40=(4+0)=4 |
60=(6+0)=6 |
|
Далее, см. п.2: Сопоставляем этот объект (и его движение) с другим подобным (или не подобным) объектом.
Оказывается наши насекомые, имеющие разный размер (1см, 2см, 3см), летают РАЗНЫМ СПОСОБОМ?!!
Нумерологическое преобразование длины пройденного пути выявило закономерности трёх разных типов движения (полёта)!?
Но, мы ведь нигде не ошиблись в расчётах, а процедуру нумерологического сокращения тоже применили одинаково ко всем данным, фазам и ко всем трём объектам.
Что касается метода соизмеримого сопоставления, то и здесь нет никакой крамолы, ибо так делают и в обычных расчётах. Тогда в чём же фокус? Откуда получились три разных вида закономерностей, повторяющихся после каждой 9 фазы движения?
А фокуса – нет! Просто – РАЗМЕР ИМЕЕТ ЗНАЧЕНИЕ! И смысл!
Из данных расчётов, зафиксированных в таблице № 1, мы со всей формальной строгостью вынуждены заключить следующее:
1. Движение трёх разных (по размеру) объектов (на любой (!) траектории их движения) отличается тремя разными типами закономерностей, которые имеют, однако, одинаковый для всех объектов циклический характер.
2. Фазы движения (по условиям эксперимента) – это промежутки времени, за которые любой из трёх объектов успевает пролететь расстояние, равное длине своего тела.
3. Числовые данные (в строках одинаковых фаз) показывают общий путь, пройденный каждым телом на момент завершения любой из фаз движения.
4. Разумеется, с учётом разной индивидуальной скорости каждого из тел; при этом потраченное время в данных таблицы никак не учитывается. То есть, Время исключается из рассмотрения. Однако, зато, мы получаем возможность корректного сопоставления пространственных характеристик движения трёх разных тел между собой.
5. Таким образом, мы выявили именно пространственные отличия в движении трёх разных объектов, которые сами по себе имеют три разных пространственных размера.
6. Выявление факта наличия трёх разных типов движения объектов стало возможным только в результате применения т.н. «нумерологического сокращения» всех числовых данных таблицы № 1, которые сами были получены строгим математическим расчётом.
7. Из изложенного выше необходимо заключить, что операция «нумерологического сокращения» числовых данных позволила увидеть в движении пространственных тел новые закономерности, которые обычной механикой и физикой НЕ ОБНАРУЖИВАЮТСЯ.
Следующий, это п. 3: Изучаем внешние проявления объекта в среде подобных (или имеющихся) объектов, а также характерные взаимодействия исследуемого объекта
Теперь мы попробуем ещё больше проявить и проанализировать обнаруженные феномены движения и попытаемся дать им своё объяснение.
Для этого посмотрим на столбцы таблицы № 1 снова.
Раз получилось так, что у всех трёх тел есть формально одинаковое количество «фаз движения», то почему бы нам не отобразить все три типа движений, так сказать, на едином поле.
Пусть таким полем будет некий лимб с 9-ю равными отрезками – делениями.
См. Рис. 1,2,3,4.
 |
| Рис. 1 |
Рис.1 Лимб - 9, на котором будет проводиться отображение табличных данных.
В качестве исследуемых данных мы возьмём жирные цифры каждого их столбцов Таблицы 1 (для всех 3-х объектов), то есть длины пройденных путей по фазам движения каждого из трёх тел.
При этом каждая из фаз будет последовательно начинаться с того числа, которое есть в начале движения у каждого объекта, а на лимбе – с той цифры, которая соответствует этому числу. Следующая фаза даст нам новую цифру, которую мы найдём на лимбе и проложим следующий отрезок, от последней цифры предыдущей фазы движения.
В итоге мы будем иметь некоторую условную траекторию на Лимбе-9, которая каким-то образом отразит безусловную траекторию движения, зафиксированную в таблице № 1 движений насекомых.
Поскольку даже невооружённым глазом из таблицы видны три разных закономерности в движении разных тел, то с помощью Лимба-9 мы сможем эти закономерности выявить совершенно отчётливо. А теперь посмотрим на полученные графики-лимбы.
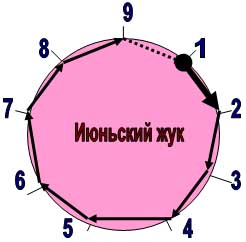
Отображение траектории полёта июньского жука (L=1cм)
 |
| Рис. 2 |
На этом лимбе первая (жирная стрелка с точкой) означает начало полёта жука и начинается она с цифры = 1, так кок это есть длина самого жука в начале его пути.
А заканчивается 1-я фаза движения на цифре=2, так как жук достиг в конце 2-й фазы движения длины пути, которая равна ДВУМ длинам его тела. Следующая стрелка будет в точке=3 и так далее.
Из конечной точки = 9 цикл повторяется, а поэтому стрелка, отображающая переход
от 9 к 1, показана в виде пунктирной стрелки, чтобы обозначить, тем самым, место перехода к новому циклу. Аналогично будут нарисованы и другие лимбы.
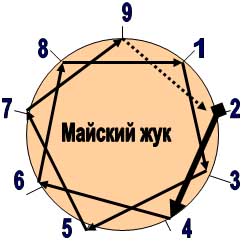 | 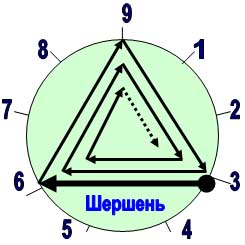 |
| Рис. 3 | Рис. 4 |
Как мы и предполагали, различие в характере движения трёх «разнокалиберных» объёктов на Лимбах-9 выявилось ещё более отчётливо (см. Рис. 2,3,4).
Возникает законный вопрос: « Неужели т.н. “нумерологическое сокращение” действительно позволяет отличать (назначать) различных насекомых в разные группы двигающихся тел? Что-то не верится!»
А если бы мы тем же самым методом сопоставляли автомобили с длиной кузова в 1, 2 и 3 метра, но, в самих автомобилях поставили бы двигатели с мощностями ровно в обратной пропорции?! В самую маленькую – самый мощный мотор, а в самую большую – самый слабый мотор? И что тогда покажут эти лимбы? Чушь, какая-то!
Так подумает здравомыслящий читатель и будет по-своему прав.
Действительно, использованные приёмы и способы отображения как-то иначе, чем обычно, связаны с манерой (характером) движения насекомых или автомобилей.
Тем не менее, они отображают некий реальный, но скрытый характер движения, и, как было отмечено выше – вид пространственных характеристик движения. Это отображение не прямо самих объектов исследования, но цифр, связанных и отображающих характеристики специфически определённых движений объектов.
Тот факт, что в нашем мысленном эксперименте заранее был исключён фактор времени (мы не измеряли скоростей, а только пути, который соизмеримы с размерами движущихся насекомых), позволил получить ОТНОСИТЕЛЬНЫЕ параметры движения насекомых. И сопоставлять три вида насекомых. Но это могли быть и очень разные объекты. Это могли бы быть, например, - жук и автомобиль. Это одно важное отличие!
Другое отличие в том, что у нас совершенно отсутствовали (по условиям эксперимента) такие параметры движения объектов, как направление их полёта, скорости их движения на каждой из фаз (жук или шершень могли зависать над цветками, двигаться назад, вверх, вниз, равноускоренно или равномерно - как угодно). По условиям нашего эксперимента не накладывалось практически никаких ограничений на способ полётов наших насекомых. И это тоже весьма важно!
Тогда, что же выражают собой графики и лимбы, которые были нами получены и нарисованы?
При всей парадоксальности ситуации они действительно отражают движение реальных объектов (жуков и шершня), вот только какого уровня это отображение? И в чём его смысл?
Поясню это другим суждением. Мы могли бы, например, произвести какую-нибудь другую процедуру по преобразованию исходных данных (см. таблицу № 1) движения и получить самые невообразимые выходные данные.
После такого преобразования исходных данных движения объектов в таблице № 1 результаты были бы ещё более неправдоподобны и удивительны. И любой здравомыслящий читатель возмущался бы не менее бурно, чем сейчас.
Таким образом, весь секрет странных картинок на лимбах заключён именно в процедуре «нумерологического сокращения», которую придумал сам Пифагор, еще 2500 лет назад.
Авторитет Пифагора за эти годы ничуть не пошатнулся, а значит, изобретатель арифметических ПРОЦЕДУР (сложения, вычитания, умножения и деления) профаном никак не был и он точно знал скрытый смысл обсуждаемой манипуляции, а также сферы её применения при анализе числовых данных.
Как то так вышло, что он либо не раскрыл данного секрета своим ученикам, либо они сами его скрыли, либо секрет был утерян (например, из-за непонимания его сущности). Отказываться от попыток «раскусить» эту тайну, я думаю, нам не следует! Расследование должно продолжаться.
Надо искать разгадку самим. Единственный проведённый нами мысленный эксперимент достаточно прост для того, чтобы уловить идею этой странной операции (манипуляции с числами), придуманной Пифагором.
Если мы немного отвлечёмся от сути эксперимента и будем помнить только то, что речь в нём шла об относительном движении и сопоставлении движений по данным таблицы 1, то мы, прежде всего, должны отметить собственную значимость наших числовых экспериментов.
Во-первых, разве это не удивительно, что самоотложение (длины тела на собственной траектории движения) при разных абсолютных длинах (у всех 3-х объектов) даёт нам совершенно разные закономерности (см. лимбы 2, 3, 4).
Я применил здесь термин самоотложение.
Однако, можно было бы выразить ту же ситуацию и другими словами. Например, подошли бы такие слова: самосложение, самоумножение, репликация самого себя, клонирование при жизни, саморепликация на траектории).
Таким образом, с чисто формальной, числовой позиции, мы получили диаграммы (на лимбах), отражающие процессы саморепликации движений объектов с разными исходными параметрами («размерами насекомых»). Вот это следует запомнить.
|
Мы получили методику обработки данных (и средство отображения) исключительно для (само) реплицирующихся процессов!
|
СТОП! СТОП! СТОП!
А ведь такого рода процессов в Природе – тьма-тьмущая! Ай, да Пифагор!
Недаром сам Пифагор говорил своим ученикам, что его наивысшее научное достижение – это Таблица умножения! Что? Что? Причём здесь Таблица умножения?
Господи, неужели я не сказал, а вы сами не увидели, что наша с Вами исходная Таблица №1 это и есть таблица умножения первых трёх цифр. Посмотрели? Убедились? Ну и отлично.
Итак, Пифагор из глубины 25 веков подарил нам, нашему миру изумительное средство для решения тех гигантских проблем, которые стоят перед нашим временем. Его таблица имеет космическое значение, если только понимать скрытый смысл тех движений, которые она отображает!
Вспомните о компьютерном «Кошмаре Перебора», который не позволяет решать в режиме “on-line” задачи по распознаванию визуальных оптических образов (топографических карт местности, космических фотоснимков, портретов, отпечатков и других следов преступлений)!
В этой сфере мы сейчас в том же положении, как во времена ДО изобретения арифметической операции УМНОЖЕНИЯ. Всё приходилось СКЛАДЫВАТЬ, причем вручную и многократно. «Склады» фараонов и магараджей были переполнены. Древняя «логистика» - не работала. Те, кто знал законы умножения, были настоящими магами и волшебниками. И это не преувеличение, что за это Знание магараджи древней Индии отдавали свои кровные пол - царства. Это исторические факты!
К слову сказать, я раскрою ещё одну тайну Пифагора, тайну о его методе «нумерологического сокращения». Как мы могли убедиться выше, все эти необычные результаты в нашем эксперименте получились благодаря соединению двух открытий Пифагора – таблицы умножения и нумерологического сокращения.
Если бы мы использовали в отношении чисел Таблицы №1 любые арифметические операции (ну, вы помните все семь арифметических действий с числами), то результаты преобразования данных Табл.1 не были бы столь экзотическими. Можете проверить самостоятельно.
А поэтому следует заключить, что
операция «нумерологического сокращения по Пифагору»
НЕ ЯВЛЯЕТСЯ АРИФМЕТИЧЕСКИМ действием.
Это сугубо иная математическая манипуляция (процедура) по преобразованию чисел,
имеющая свой особый смысл и свою область применения.
|
Эта операция позволяет выявить (раскрыть) иные стороны и математические характеристики реальных числовых процессов. Вопрос – каких именно?
То есть, при применении к числам, отражающим реальные объекты (либо количественную сторону их качеств!) процедура нумерологического сокращения выявляет (обнажает, вскрывает, демонстрирует) скрытую сущность любых чисел.
Вот почему эту же процедуру часто называют по-другому: «извлечение нумерологического корня числа» или «извлечение «теософского корня числа».
Эзотерические и оккультные пояснения здесь более чем уместны, так как не стоит забывать, что научными знаниями в те далёкие века занималось «ведомство древнеегипетских (и других) жрецов», причём самого высшего уровня.
А Пифагор Самосский - сам был таким жрецом, который осмелился нарушить клятву и табу на распространение (среди невежд и профанов) тайных жреческих знаний, включая сюда и знания по математике.
Заключительный вывод данной статьи состоит в том, что наш мысленный эксперимент и его анализ позволяют сказать, что при наличии реальных исходных данных по любого рода процессам движения, кроме традиционных методов анализа мы можем применять новые процедуры и способы, основанные на пифагоровском подходе к числам, о котором повествует данная статья.
|