Общая формула синтеза новых чисел (изомеров) на основе исследуемых (147,258, 369) такова:

• ЕслиВершины соответствующих треугольников, вписанных в Лимб-9 и отмеченнвх дугами умножать на соответственный коэффициент (показан над дугами), то суммы треугольников будуи различаться на число = 819. При этом - 819 = 9*91 = 7*9*13 = 3² х 7 х 13;
• Это, в частности, означает, что поворот треугольника на 1/9 окружности, т.е. на 360⁰/9 = 40⁰ вызывает увеличениесумм на число 819.
• Значит, в пределах дуг, относящихся к коэффициентам, мы имеем прирост на число 1630 = 2*7*9*13.
• Минимальная разница между числами в нашей таблице (в пределах любой из 3-х групп изо-чисел) равна числу – 216 = (6 х 36) = 6³ .
• Числа 819 и 216 образуют пропорцию: 819/216 = 345/91 = 91/24 = (13х7) /(2х12);
• Эта пропорция также равна, соответственно, 819 / 216 = 3,7916666 = ln (133 /3);
• Вся таблица прямо-таки переполнена ПРОСТЫМИ числами (выделены жирным шрифтом)

Сумма чисел всех групп равна 73710 = 7*10530 = 7*13*810 = 7*5*13*162 =2*5*7*13*9*9 = 2*5*7*13*9² ;

• ЕслиВершины соответствующих треугольников, вписанных в Лимб-9 и отмеченнвх дугами умножать на соответственный коэффициент (показан над дугами), то суммы треугольников будуи различаться на число = 819. При этом - 819 = 9*91 = 7*9*13 = 3² х 7 х 13;
• Это, в частности, означает, что поворот треугольника на 1/9 окружности, т.е. на 360⁰/9 = 40⁰ вызывает увеличениесумм на число 819.
• Значит, в пределах дуг, относящихся к коэффициентам, мы имеем прирост на число 1630 = 2*7*9*13.
• Минимальная разница между числами в нашей таблице (в пределах любой из 3-х групп изо-чисел) равна числу – 216 = (6 х 36) = 6³ .
• Числа 819 и 216 образуют пропорцию: 819/216 = 345/91 = 91/24 = (13х7) /(2х12);
• Эта пропорция также равна, соответственно, 819 / 216 = 3,7916666 = ln (133 /3);
• Вся таблица прямо-таки переполнена ПРОСТЫМИ числами (выделены жирным шрифтом)

Сумма чисел всех групп равна 73710 = 7*10530 = 7*13*810 = 7*5*13*162 =2*5*7*13*9*9 = 2*5*7*13*9² ;

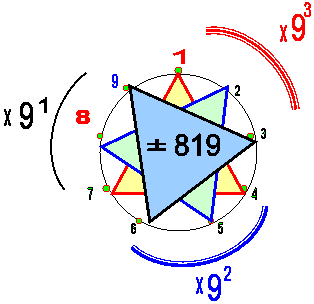Рис. 1

Таким образом, исследование показывает, что изомеры чисел - констант (147), (258) и (369) содержат при своих преобразованиях (в степенные ряды) и формируют результаты на основе ПРОСТЫХ чисел.

Это, в свою очередь, подтверждает фундаментальный характер чисел-констант как самих по себе, так и в связи с их связью с простыми числами, загадка которых не раскрыта и по сей день.

Наложим теперь на наш рисунок фигуру т.н. эннеаграммы Гурджиева и увидим, что выделенные нашими дугами точки на Лимбе-9 соответствуют ТРЁМ толчкам (инициациям) принятым в эзотерической интерпретации абриса фигуры Гурджиева.

Первый толчок имеет место в диапазоне цифр (1 –3), второй толчок в диапазоне цифр (4 – 6), а третий толчок – в диапазоне цифр (7 –9)..

Центры этих диапазонов приходятся, соответственно, на цифры 2 –5 – 8.

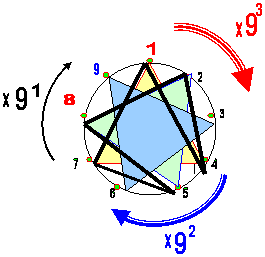Рис. 2

Известный всем треугольник 3-6-9, который (как бы) не задействован в абрисе Гурджиевской эннеаграммы, на нашем рисунке получает вполне логичную интерпретацию. Вершины данного треугольника ВСЕГДА совпадают с концами наших дуг, объединяющих собою числа – изомеры, входящие в одну группу, каждая из которых отличается своей числовой «мощностью».

Тем самым смысл завершения дуги – ПЕРЕХОД к другой группе движения.

НЕ ОХВАЧЕННЫЕ дугами интервалы на Лимбе – 9 – это промежутки (3-4), (6-7) и (9-1). Нумерологические значения сумм в этих интервалах, соответственно: [7]. [4] и [1], т.е такие, что вновь выявляют собой число – константу 147 (в зеркальном отображении).

Таким образом можно сказать, что ПЕРЕХОДЫ в эннеаграмме в сущности по-прежнему обусловлены природой ПЕРВОЦИФР «1», «4» и «7», но только в несколько изменённой форме.

147 --- [3];

147 +111 = 258

258 --- [6];

258 + 111 = 369

369 --- [9];

Конец 1-го Цикла.

369 + 111 = 480

480 --- [3];

480 +111 = 591

591 --- [6];

591 + 111 = 702

702 --- [9];

Конец 2-го Цикла.

702 + 111 = 813

813 -- [3];

813 = 111 = 924

924 -- [6];

924 + 111 = 1035

1035 --- [9];

Конец 3-го Цикла.

Ниже показаны числа – константы (синий цвет) в окружении ПРОСТЫХ чисел

(они выделены жирным шрифтом):

1. 143, 147, 149, 151, 173, 174, 179       

2. 257, 258, 283, 285

3. 367, 369, 396, 397,

4. 417, 419, 471, 473*,479,                    

5. 523, 528, 529*, 582, 583*,587,

6. 631, 639, 641, 691, 693,

7. 713*, 714, 719, 741, 743

8. 823, 825,  852, 853,                              

9. 936, 937,  953, 963, 967,                     

Существует строго определённая, естественная комбинация в размещении чисел – изомеров, благодаря которой выявляются реальные и интересные закономерности взаимоотношений чисел- констант.

Ниже будут приведены результаты изысканий на эту тему.

Они представляют собой геометрические построения с оцифровкой и соответствующими расчётами

Эти изыскания относятся к проблеме поиска правильного расположения Первоцифр. Однако мы начнём с моих любимых чисел – констант (147, 258, 369)

На рисунке ниже даётся итоговый, обобщённый рисунок по размещению указанных чисел в системе 3-х окружностей, имеющих 3 точки пересечения. Но, вначале – упрощённая схема.

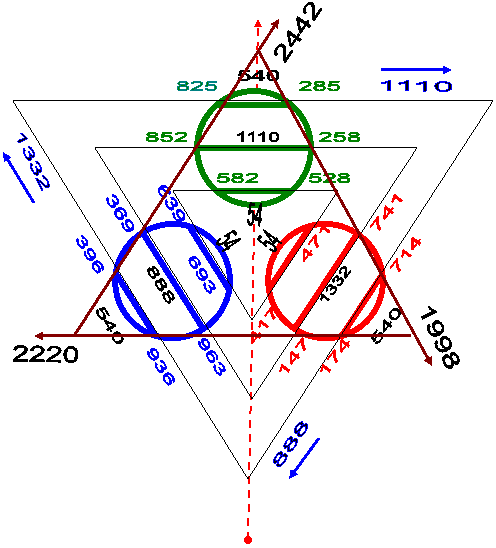Рис. 3

А теперь мы рассмотрим более детальную картинку внутренних связей чисел на рисунке, где в системе трёх окружностей проведены все линии и рассчитаны суммы и разницы соседних узлов.

Там же найдена ось симметрии данной геометрической системы с исследуемыми числами и выделены наиболее интересные линии.

Кроме того, показаны линии, которые пересекают рисунок по диагональным направлениям и подсчитаны суммы пересечённых узлов.

Как можно видеть, система чисел – констант даёт весьма сбалансированную картину, которая позволяет убедиться в том, что взаимодействие исследуемых чисел именно в таком порядке раскрывает скрытый механизм этого взаимодействия.

В частности, данная картинка позволяет записать следующие закономерности:

1. (369+936+693) +(963+396+639) = 1998 + 1998 = 3996;      3996:3 = 1332;
2. (147+471+714) + (741+174+417) = 1332 = 1332 = 2664;     2664 : 3 = 888;
3. (258+528+825) + (852+582+285) = 1611 + 1719 = 3330;     3330 : 3 = 1110;
4. 1110 х 3 = 3330; 888 х 3 = 2664; 1332 х 3 = 3996;
5. 3330 + 2664 + 3996 = 9990!
6. Или (888 + 1110 + 1332) х 3 = 9990!

Кроме того, рисунок вскрывает и такие соотношения:

1. (471 + 528) = 999 = 9 х 111;
2. (417 + 693) = 1110 = 10 х 111;
3. (639 + 582) = 1221 = 11 х 111;

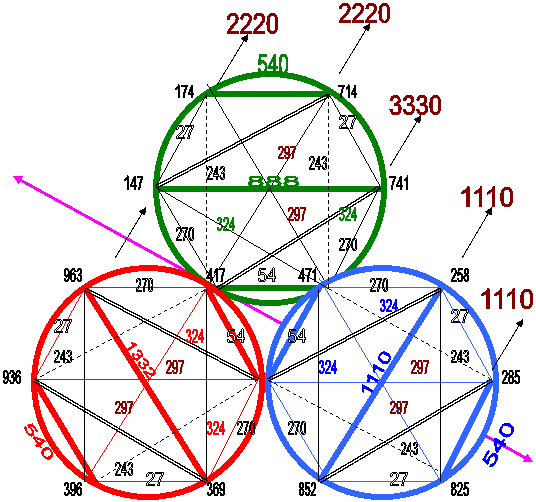Рис. 4

В итоге мы получаем возможность осуществить правильный спиральный обход всех чисел-констант (всех чисел изоморф) по траектории – из центра к периферии по следующему маршруту:

(417-471)-(528-582)-(639-693)-(147-741)-(258-852)-(369-963)-(174-714)-(285-825)-(396-936)

Последний раздел в этой главе – исследование комбинаторики, которая возможна с числами-конмтантами.

Эти данные помогут нам в дальнейшем для составления эквивалентных формул переходов из одних систем обхода – в другие системы.

Путём экспериментов были найдены универсальные формулы, позволяющие осуществлять комбинаторные перестановки в трёхзначных числах. И, в частности, в числах – константах.

Формулы эти выглядят следующим образом:

Пусть в трёхзначном числе цифры заменены на буквы, т.е. мы имеем число вида «АВС», где А, В, и С, в последствии, могут быть заменены на любые цифры.

Тогда справедливы следующие формулы:

1. (ВСА – АВС) = (ВСА – АСВ) + (АСВ – АВС);

2. (САВ – АСВ) = (ВАС – САВ) + (АСВ – ВАС);

3. (СВА – ВАС) = (СВА – САВ) + (САВ – ВАС);

а также:

1. (АСВ – СВА) = (АСВ – ВСА) + (ВСА – СВА);

2. (АВС – САВ) = (АВС – ВАС) + (ВАС – САВ);

3. (ВАС – ВСА) = (САВ – ВСА) + (ВАС – САВ)

Рассмотрим применение этих формул применительно к изоморфам константы 147.

Пусть А = 1, В = 4, С = 7.

Тогда:

(471 - 147) = (471 – 174) + (174 –147) --- 324 = 297 + 27 (!)

(741 – 417) = (741 – 714) + (714 – 417) --- 324 = 297 + 297 (!)

(714 – 174) = (417 – 174) + (714 – 417) --- 540 = 243 + 297 (!)

Пусть теперь А = 2, В = 5, С= 8.

Тогда:

( 582 – 258) = (582 – 285) + (285 – 258) --- 324 = 297 + 27

(852 – 528) = (852 – 825) + (825 – 528) --- 324 = 27 + 297

(825 – 285) = (528 – 285) + (825 – 528) --- 540 = 243 + 297

Пусть теперь А = 3, В = 6, С= 9.

Тогда:

(693 – 369) = (693 – 396) + (396 – 369) --- 324 = 297 + 27

(963 – 639) = (963 – 936) + (936 – 639) --- 324 = 27 + 297

(936 – 396) = (639 – 396) + (936 – 639) --- 540 = 243 + 297

Все величины, указанные в формулах мы можем увидеть на рисунке 3 и рис 4.