В этой статье представлены некоторые результаты исследований, связанных с применением нового способа умножения, который изобретён к. ф.н. Василием Ивановичем Оконешниковым. Учёный утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. Лучший вариант - это девятеричная система. Все данные располагают в девяти ячейках, как в кнопках калькулятора.

Напомним суть этой новой процедуры (манипуляции),, придуманной ОКОНЕШНИКОВЫМ В. И., которую далее будем для краткости именовать по имени создателя ПОК. А затем, пойдём дальше.

1. Прежде всего, уточним, что число 15647 – множимое, а цифра 5 - множитель.
2. С помощью цифр множителя (5) определяется (выбирается) малый квадрат (3х3 ячейки) из которого далее будут выписываться в один ряд числа.
3. Цифры множимого (в порядке их обычного чтения) – это указатели на те ячейки, из которых поочерёдно делаются выписки в ряд.
4. Из малой ячейки, которая соответствует множителю, т.е. пятёрке 5 (см. красные большие числа в квадратах 3х3), выбираем числа, соответственно цифрам множимого (15647) - числа по порядку: то есть единице, пятёрке, шестёрке, четвёрке и семёрке.
5. Получаем специально выписанный ряд чисел : 05 25 30 20 35
6. Почему именно эти числа? Потому, что каждый из малых квадратов (3х3) имеет постоянную и одинаковую нумерацию. Порядок нумерации ячеек здесь такой: из левого нижнего угла (это = 1) направо - по нижней строке, затем переход в левую клетку средней строки (это цифра = 4) и так далее. Получается обход «Змейкой»
7. Левая цифра (самого первого) числа, выписанного из ячейки №5, на которые указала первая из всех разрядов цифра «множимого» (у нас - ноль) оставляется без изменений, а следующие складываотся, как это показано на отдельном рисунке в самом низу.
8. Последняя цифра из выписанного ряда чисел также оставляется без изменений.

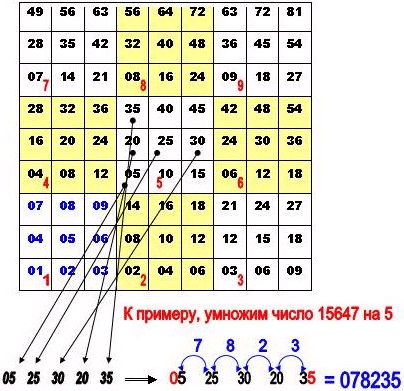Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

Из нового метода (ПОК) мы позаимствуем оригинальный метод формирования итогового результата, а именно сложение с определённым принципом группировки цифр слагаемых чисел (см. иллюстрацию выше).

Данное исследование относится к области эзотерической математики. Поэтому первым объектом его внимания, конечно же являются самые главные эзотерические числа – числа самой Монады.

Я намереваюсь, таким образом, провести исследование чисел: 369 – 147 – 258 – 369 с использованием новой манипуляции с исходными, анализируемыми числами.

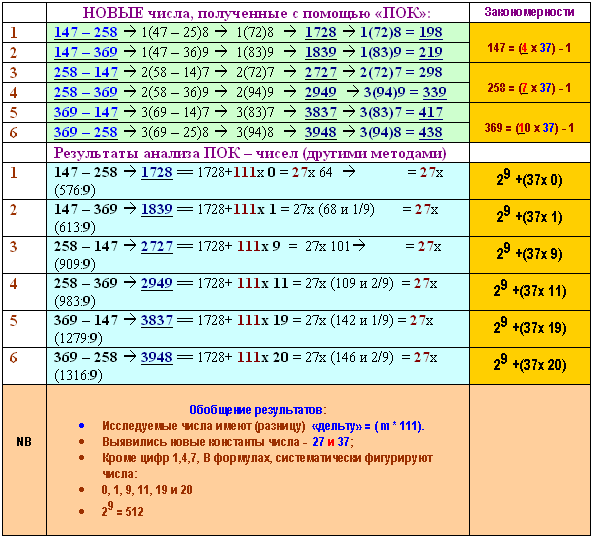
Правило №1 – это специфическое сложение (как в ПОК) которое будет проводиться для всех чисел монады, взятых попарно (см. табл.1). Всего 6 таких пар. Пары обозначаются, например, так: 369 – 258.

Правило №2 новой манипуляции будет содержать требование о необходимости повторения Правила 1 в отношении промежуточных результатов, если эти результаты не будет давать новые числа с такой же размерностью, как и исследуемые (трёхзначные числа).

Правило №3. Получаемые итоговые числа анализируются на предмет связей друг с другом, на наличие общих множителей, методом лимбов и на предмет выявления иных закономерностей.

Таблица 1

На этом этапе на лимб 9 нанесена оцифровка числами, которые получены путём перестановок цифр в исходных, анализируемых числах Монады.

Эти числа расставлены на лимбе 9 так, чтобы по отношению к исходному числу другие числа можно было различить «направлением циркуляции». Например: 147 – исходное число.

Если мы переставим 1 на место самого младшего разряда и получим число 471, то это будет условное (см. Рис. 2, ниже) движение против часовой стрелки.

Поскольку возможно другое графическое отражение этого же процесса перестановки, то такой перевод цифры (когда стрелка перевода цифры находится сверху!) мы принимаем, как НЕ ВЕРНОЕ!

Рис. 2

По ВЕРНОЙ мнемонической схеме (Рис 2) превращение исходного числа 147à714 будет переводом самого младшего разряда в положение самого старшего разряда и одновременно – движением против часовой стрелке.

Превращения остальных чисел 258 à 582 – это движение против часовой стрелки

Остальные превращения квалифицированы в таблице 2.

Таблица 2

В соответствующей последовательности (при обходе по часовой стрелке всех трёх основных вписанных треугольников) расположим исходные и преобразованные числа на лимбе 9 (см. таблицу 3).

Таблица 3

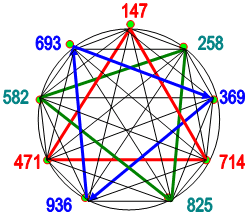Рис. 3   Лимб 9.

А теперь, - числовые закономерности чисел Монады, найденные (на основе анализа лимба 9), которые отражены в Таблице 4

Таблица 4. Закономерные отношения чисел Монады

Итогом исследований, проведённых в данном исследовании являются различные закономерности и соотношения, которые связывают три главных числа монады.

В задачу автора не входила, в данном случае, эзотерическая интерпретация полученных результатов.

Цель этого исследования состояла в нахождении и апробации разных - новых и старых математических манипуляций, способных выявлять новые числа и связанных с главными «монадными» числами.

Тем самым, автор предоставляет более квалифицированным эзотерикам и исследователям почву и базу для новых смысловых обобщений и (в целом) для реконструкции и восстановления эзотерической математики.