Исследование цифр «1, 3, 7» в числах
| |
Это похоже на вопрос ребёнка к мудрому учителю. Ответ будет прост (чтобы ребёнок понял), но «кухня» формирования такого ответа – неизмеримо сложнее сознания ребёнка.
Число – вершина айсберга фундаментальных закономерностей, в которые мы ещё даже не углублялись…
/ КАА / |
В этой статье представлены мои ранние способы исследования цифр. В частности, цифр «1,3,7» объединённых в число 137; и ещё один (дополнительный) способ исследования внутренней структуры чисел, в котором изюминкой является применение простых дробей.
Эти же способы пригодны и для изучения знаменитой константы «317», которую ввел в научный оборот Велимир Хлебников в своей Теории Времени.
Однако, изложу всё по порядку.
Сущность способа заключается в следующих шагах и действиях:
Шаг 1. Выбираем исследуемое число и устанавливаем все его изоморфнве образы (далее – изоморфы), т.е. пишем все комбинации с перестановками цифр, имеющимися в данном числе. Получаем исходный набор чисел для дальнейших исследований.
Шаг 2. Вычисляем нумерологический корень исходного числа (он будет одинаков и для чисел - изоморфов).
Шаг 3. Каждое из полученных в наборе чисел делим на число 11, что эзотерически означает сопоставление этого числа с Абсолютом. (Мы как бы устраеваем исследуемому числе «очную ставку» с самим Абсолютом, которая должна «высветить» всю подноготную этого числа. Для больших чисел полезно брать в качестве «делителя» на «11», а число «111», соответствующее Вселенной.
Шаг 4. Полученные десятичные дроби (используем калькулятор) НЕОБХОДИМО выразить (преобразовать) в виде ПРОСТЫХ ДРОБЕЙ. Это очень важно, поскольку именно (и только!) простые дроби выявляют скрытых участников процессов взаимодействия между числами.
Шаг 5. Числа – изоморфы (в виде целых и простых дробных частей) располагаем на Лимбе такой же кратности, что и число изоморфов. Если для исходного 3-х значного числа мы получаем всего 6 изоморфов, то и лимб для их отображения будет иметь всего 6 точек на окружности (Лимб-6)
Шаг 6. Методом подбора и предварительных расчётов расставляем числа-изоморфы на Лимбе так, чтобы добиться симметричного числового баланса между ними и относительно оси общей симметрии
Шаг 7. Рисуем окончательную картинку Лимба с расставленными на его точках числами и начинаем анализировать эту картинку и делать далеко идущие выводы J….
В качестве ОБЪЕКТА мы будем исследовать весьма примечательное число 137, – за которым одни исследователи усматривают т.н. «Константу тонкой структуры Вселенной», другие – нумерологическое число Смерти, третьи - образы из пушкинской «Пиковой дамы» - карты: Тройку, Семёрку и Туза.
Вот мы и посмотрим на данное число, в частности, через призму нового способа.
**********
Исследуемое число – 137 имеет нумерологический корень = 1+3+7 = {11} --- [2];
Число 137 имеет следующий набор изоморф: 137, 173, 317, 371, 713, 731 (одно из чисел-изоморф – Хлебниковская константа – 317)
Нарисуем таблицу, в которой было бы удобно отображать дальнейшие результаты.
| |
Деление на «11» |
Число с простыми
дробями |
Группировка
чисел парами |
| 137 |
12,4545(45) |
12 5/11 |
* |
| 173 |
15,7222(2) |
15 8/11 |
+ |
| 317 |
28,8181(81) |
28 9/11 |
** |
| 371 |
33,7272(72) |
33 8/11 |
+ |
| 713 |
64,8181(81) |
64 9/11 |
** |
| 731 |
66,4545(45) |
66 5/11 |
* |
После группировки чисел по парам получим 3 такие пары чисел:
(137 – 173), (173 – 371), (317 – 713);
Общая сумма всех чисел (по-парных): 310 + 544 + 1030 = 1884 –> {21} –> [3];
Баланс сумм этих пар чисел (левый и правый) выполняется только в таком раскладе:
«Левые»: 137 + 371 + 713 = 1221;
«Правые»: 731 + 317 + 173 = 1221;
Обратим внимание, что: 1221 : 11 = 111 (!), где 111 – число Вселенной.
Вычисление баланса позволяет перейти к построениям на Лимбе-6.
И здесь возможно несколько способов расстановки чисел на лимбе:
- По признаку взождения в левые и правые (см. выше)
- По признаку зеркального отображения цифр в парах чисел
- По признаку «большее числе – напротив меньшего»
- По возрастанию (уменьшению) величины числа
- И другие методы сортировки и классификации чисел
Вот, например, расположение по признаку баланса правых и левых:
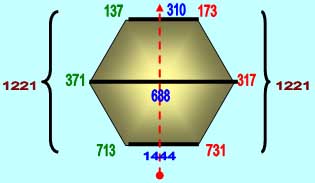 |
| Рис. 1 |
А это (ниже) - пример оцифровки по принципу зеркальности:
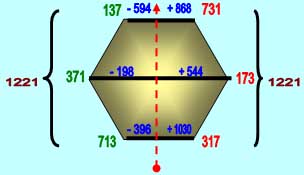 |
| Рис. 2 |
В одном из своих исследований я нашёл эмпирическую формулу представления для чисел – изоморфов. Согласно этой формуле для числа 137 можно записать следующее соотношение:
(731 – 137) = (713 – 317) + (371 – 173) => (594) = (396) + (198)
Эта формула также позволяет произвести оцифровку лимба. Как можно увидеть (Рис.3) – здесь осуществляется группировка чисел попарно, а точнее по признаку их зеркальности.
Остановимся на одном из вариантов более детально. На Рис.3 (ниже) показана оцифровка, где связи между числами на лимбе показаны в виде разности значений пар чисел
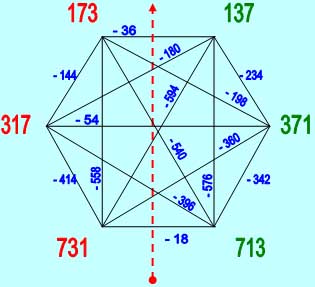 |
| Рис. 3 |
А на Рис.4 (см. ниже) все числа и величины сумм пар этих же чисел разделены на число «11» и представлены в виде целых чисел с простой дробью (итог – выделен красным цветом) на линиях, соединяющих пары чисел.
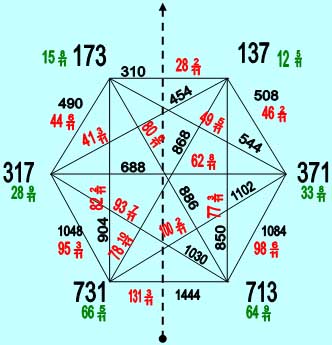 |
| Рис. 4 |
И, наконец, опираясь на обнаруженное свойство равенства одной половины чисел – другой половине, построим новый лимб, где объёдиним эти тройки чисел геометрически в треугольники, которые имеют противоположную ориентацию вершин.
При этом прибегнем к ещё одной маленькой нумерологической хитрости, которую я называю: НЕПОЛНОЕ НУМЕРОЛОГИЧЕСКОЕ СОКРАЩЕНИЕ.
Суть его в том, чтобы представить числа из нашего исследуемого набора в несколько иной форме:
Конкретно: 137 a (13)7 a 47;
317 –> (31)7;
371 –> (37)1;
731 –> (73)1;
713 –> (71)3;
173 –> (17)3;
Цифры в скобках сложим нумерологически и получим такие соответствия между исходными числами и новыми, синтезированными:
137 –> «47»;
317 –> «47»;
371 –> «101»;
731 –> «101»:
713 –> «83»;
173 –> «83»;
Теперь, благодаря «неполному нумерологическому сокращению» мы получаем возможность проставить некий хитрый индекс «Х» между теми числами-изоморфами, которые его порождают.
После этого заметим, глядя на Рис.5, что незаполненные места можно заполнить такими же хитрыми индексами, если объединять уже не первые цифры чисел, а последние две цифры.
Такими новыми индексами мы и дополним картинку, после чего вычислим нумерологические корни чисел – индексов.
В итоге получим вот такую картину:
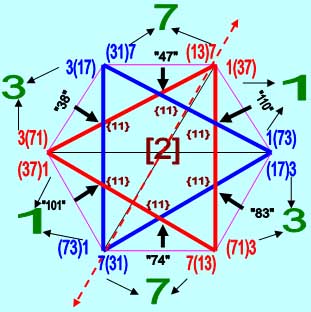 |
| Рис. 5 |
Как можно убедиться по этой картинке, каждая индивидуальная расстановка (оцифровка) числами из набора чисел - изоморфов даёт новую информацию и позволяет выявлять – с какими числами корреспондируют исследуемые, а значит и Исходное Число.
В частности, можно видеть, что знаменитая Хлебниковская константа 317 и столь же знаменитое число 137 входят в совершенно разные тройки чисел: (317, 173 и 731) или (137, 371 и 713), что означает их принадлежность к двум разным (если вообще не к противоположным – А.К.) закономерным подсистемам.
В то же время числа 137 и 317 – системно взаимодополняющие числа!
А вот «прямыми родственными» к числу 317 являются числа одной
с ним тройки – 173 и 731.
И такие цифры встречаются в исследованиях велимироведов.
От себя могу добавить ещё ряд найденных числовых соотношений
(в коллекцию велимироведов):
е1/137 = (29:24)1/60
е = (318:317)317
ln(365/24 – 14) = 60:317
365:317 ~ 317:237
Последняя картинка (Рис.5) отличается исключительной сбалансированностью и симметрией, а нумерологические («хитрые») индексы позволили выявить неслучайность этой сбалансированности и принятой нами оцифровки.
Выявление правильной оцифровки – важнейший момент такого рода исследований чисел, а поэтому я уделяю столь большое внимание примерам и способам построения лимбов (такого рода способами).
А теперь составим сводную таблицу расчётных данных.
|
Числа на лимбе |
Результат после деления чисел
на 11 |
Num |
Сумма
отдельных
пар чисел |
|
Выявленные
Простые
Числа |
|
(137) |
12(5/11) |
5 |
|
|
3 |
|
(173) |
15(8/11) |
8 |
|
11 |
|
(317) |
28(9/11) |
9 |
|
17 |
|
(371) |
33(8/11) |
8 |
|
37 |
|
(731) |
66(5/11) |
5 |
|
227 |
|
(713) |
64(9/11) |
9 |
|
389 |
|
|
|
|
|
398 |
|
(317+371) =688 |
62(8/11) |
8 |
76 х11 = 836 |
587 |
|
(731+713)=1444 |
131(3/11) |
3 |
787 |
|
|
|
|
|
877 |
|
(317+371)=688 |
62(8/11) |
8 |
140 х11 = 1540 |
Общая сумма = 3333 |
|
(137+713)=850 |
77(3/11) |
3 |
|
|
|
|
|
|
|
|
(137+731)=868 |
80(6/11) |
6 |
130 х11 = 1430 |
|
|
(173+371)=544 |
49(5/11) |
5 |
|
|
|
|
|
|
|
|
(317+713)=1030 |
93(7/11) |
7 |
204 х11 = 2244 |
|
|
(173+137)=310 |
28(2/11) |
2 |
|
|
(173+731)=904 |
82(2/11) |
2 |
|
|
|
|
|
|
|
|
(371+713)=1084 |
98(6/11) |
6 |
204 х11 = 2244 |
|
|
(317+137)=454 |
41(3/11) |
3 |
|
|
(731+371)=1102 |
100(2/11) |
2 |
|
|
|
|
|
|
|
|
(173+713)=886 |
80(6/11) |
6 |
222 х11 = 2442 |
|
|
(317+731)=1048 |
95(3/11) |
3 |
|
|
137+371)=508 |
46(2/11) |
2 |
|
|
|
|
|
|
|
|
(173+317)=490 |
44(6/11) |
6 |
|
|
Результаты:
- Периметр лимба: (137+173+317+371+713+731) = 2442 = 37 х 66
- Обе половины Лимба равны 1221 = 37 х 3 х 11. (3, 11, 37 – простые числа!)
- Параллельные пары чисел – РАВНЫ между собой:
(310+688+1444) = (508+886+1048) = (490+868+1084) = 2442
- Суммы разниц пар чисел (по периметру): (342+18+414+36+234) = 1188, а если разделить это число на 11, то получим – 1188: 11 = 108!
- Прямоугольники, выделяемые в лимбе включают в себя ПРОСТЫЕ числа:
- 310+850+1444+904 = 3508 = 4х 877; (877 – простое число!)
- 508+1102+1048+454 = 3112 = 8х 398; (398 – простое число!)
- 490+544+1084+1030 = 3148 = 4х 787; (787 – простое число!)
- Сумма сумм «прямоугольников – 3508+3112+3148 = 9768 = 264 х 37 = 24 х 11 х 37
- Большие треугольники в Лимбе:
- 454+850+1030 = 2334 = 6х 389 (389 – простое число!)
- 904+544+1102 = 2550 = 255х10 =150х 17 (17 – простое число!)
- Сумма больших треугольников (2334+2550) = 4884, т.е. равна 2-м суммам периметра.
- Малые («равнобедренные») треугольники по периметру Лимба - 6:
- 310+508+544 = 1362 = 6 х 227 (227 – простое число!)
- 508+1084+850 = 2442 = 222х11 = 37х11х6
- 1084+1444+1102 = 3630 = 330х11 (11 – простое число!)
- 1444+1048+1030 = 3522 = 6х 587 (587 – простое число!)
- 1048+490+904 = 2442 = 222х11
- 490+310+454 = 1254 = 11х114
- Суммы противолежащих, параллельных отрезков на лимбе:
- 310+1444 = 1754 = 2х 877 (877 – простое число!)
- 508+1048 = 1556 = 3х 389 (389 – простое число!)
- 490+1084 = 1574 = 2х 787 (787 – простое число!)
- Наиболее правильная оцифровка соответствует Рисунку 5 (ось симметрии – 137 – 731).
- Выявлено большое количество Простых Чисел с которыми не вполне ведомым способом, но, так или иначе, связано ИСХОДНОЕ число 137,
- Само исходное число 137 – тоже ПРОСТОЕ.
- Общая сумма всех выявленных простых чисел (см. таблицу) равна числу 3333 (!??).
- Данное исследование показало эффективность способа «Неполного нумерологического сокращения» для изучения внутренней природы чисел и, в частности, для нахождения правильной оцифровки лимба с изоморфами исследуемого числа.
- Дальнейшие исследования можно вести используя найденные простые числа и анализируя отношения между ними и Исходным числом - 137.
ЧТО ДАЮТ ТАКОГО РОДА ИССЛЕДОВАНИЯ?
1. Вспомним ситуацию в начале любого числового исследования: В начале мы имеем какую-то константу и, в лучшем случае, способы её использования (с авторскими соображениями о её смысле). Всё! Больше у нас практически ничего не имеется.
2. Нам бы хотелось знать о новом числе больше, тем паче в рамках той системы (или систем), с которыми это число сопряжено. Но откуда всё это взять?
3. Ситуация с числами так и будет находиться в глухом логическом тупике, а поиски новых связей между числами так и будут случайными блужданиями, пока мы не поставим общую задачу «с головы – на ноги».
4. Мой вывод солидарен с прозрениями Велимира Хлебникова, который неоднократно демонстрировал принцип «топологии чисел»: нет разницы в том, какую размерность имеет в рамках его концепции число 317. Это может быть и число сонетов Петрарки и число поцелуев и параметры сдвигов материков.
5. Всё подчинено числам, а «ипостась» важных (системных) чисел может быть любой. Числа определяют события, а не наоборот. Числа – вехи и изгибы реки Времени, вот только не мы (люди) поставили туда эти вехи. По счастью мы только-только начали замечать их, как дети из окна поезда, идущего в будущее. А папа Хлебников очень долго вбивал нам это в голову: «Смотрите, детки, у этой реки только одна ткань – числа». Сколько же можно повторять? Ну, не лошади же мы!
6. У любых чисел есть своя внутренняя, скрытая от невооружённых глаз, тайная структура. Увидеть её мешает проклятая догма математики о том, что число, якобы, не имеет качественной определённости. А это – наглая ложь. Им просто так удобнее. Математики просто ленятся (или не способны!) заняться исследованиями в этой сфере. Достаточно сказать, что ещё во времена Пифагора люди знали около 60 разных свойств чисел! Отдельный вопрос – как (и по каким причинам?) общая математика отошла от правильного понимания природы чисел, как объектов Природы. И будущий анализ этого вопроса будет честным детективом!
7. Когда несколько цифр проставлены в той или иной последовательности в одном числе, то происходит взаимодействие внутренних сущностей этих цифр, которое всегда связано с ещё более фундаментальными числами, чем мы можем это себе представить. Всё это очень похоже на вопрос ребёнка к мудрому учителю. Ответ будет прост (чтобы ребёнок понял), но «кухня» формирования такого ответа – неизмеримо сложнее сознания ребёнка. Число – вершина айсберга таких фундаментальных закономерностей, в которые мы ещё даже не углублялись.
8. В результате нашего исследования мы увидели, что число 317 – простое число, но мы увидели также и то, что оно органично связано (в рамках системы чисел-изоморф) с целым сонмом других простых чисел. Разве это пустяк? Каков смысл этого? Почему именно таков набор связных простых чисел? Что за этим стоит?
9. Мы увидели, что совсем не безразлично - каким способом осуществлять оцифровки лимбов в избранной системе чисел. И каждая система чисел потребует своей оцифровки для выявления скрытой информации об участниках взаимодействия.
10. Мы увидели, что последовательное применение метода выявляет некоторые обобщающие числа. Например, сумма всех выявленных в ходе исследования простых чисел = 3333 (!??). Что это? Каков смысл этой «кругленькой» суммы? Как и где её можно применить? И разве можно это назвать случайностью? Нет, скорее это - образчик нашей слепоты и недостаточной образованности в сфере научного и прикладного числознания.
11. У автора, к сожалению, нет ответов на все вопросы. Зато есть намерение идти дальше в этом направлении.
12. Присоединяйтесь, господа исследователи и сотворцы, присоединяйтесь…
|