Числонавтика
Исследование нового способа умножения
В этом разделе мы рассмотрим и исследуем новый способ умножения, о котором недавно появились сообщения.
Школьники Ульяновска научатся устно складывать и умножать миллионы, биллионы и даже секстиллионы с квадриллионами. А поможет им в этом кандидат философских наук Василий Оконешников, по совместительству изобретатель новой системы устного счёта.
Учёный утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить.
ОПИСАНИЕ ПРОЦЕДУРЫ
К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35
Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.
В итоге получаем: 078235. Число 78235 и есть результат умножения.
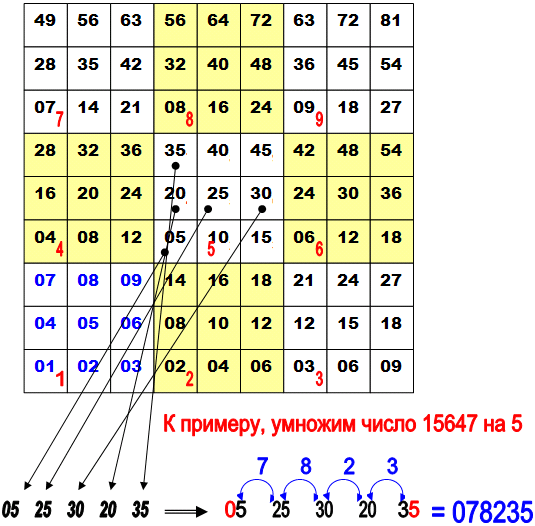 |
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Кроме того, Оконешниковым созданы девятиричные таблица умножения и таблица Менделеева. По последней, по заявлению изобретателя, его собственная шестилетняя дочь за неделю выучила все химические элементы, включая все их характеристики.
А первая же, таблица умножения, позволяет в уме «ворочать» поистине огромными числами.
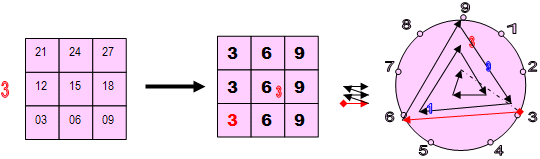
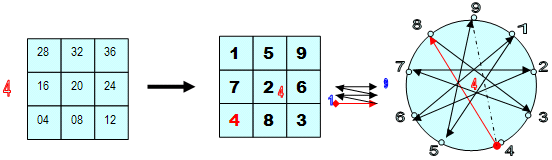
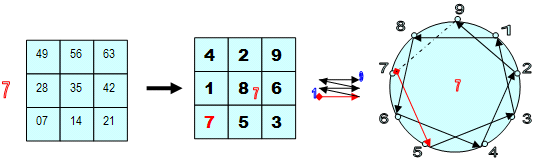
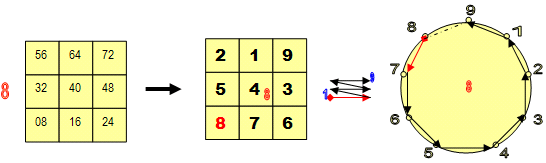
ОПЫТ 1: Что такое малые квадраты (3х3) Большой таблицы?
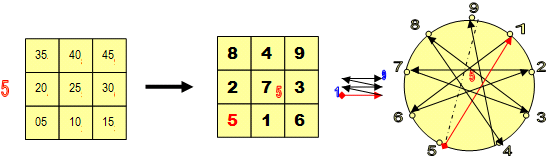 |
ИЗ «контейнера» (3х3) № 5 БОЛЬШОЙ таблицы (9х9) извлекают по очереди числа, соответствующие (слева – направо) «множимому», то есть 15647. Проще говоря, цифры множимого указывают на МЕСТА, из которых надо последовательно извлечь нужные числа.
Из 1 ячейки «контейнера» извлекают число 05, из 5 ячейки – число 25, из 6 ячейки – число 30, из 4 – 20, а из ячейки 7 – число 35.
Получаем набор чисел – заменителей числа 15647: 05-25-30-20-35 (нумерологический аналог будет равен: 5-7-3-2-8)
А затем, следует совсем ничем не обоснованная (с позиций традиционной математики) процедура (т.е. определённый порядок действий), с помощью которой досигается искомый результат умножения!
А именно:
- Первую и последнюю цифры нового набора оставляют без изменений!
- Остальные соседствующие цифры попарно складывают, выписывая их суммы.
- При получении числа >9 – цифру младшего разряда вписывают, а цифрой старшего разряда корректируют предыдущую (левую) цифру.
Поэтому, можеь быть, логичнее было бы начинать «хитрое сложение» цифр замещающего набора чисел не с слева, а справа!
А в чём состоит смысл и основание для такого «хитрого сложения»(!)? Автор метода, к.ф.н. Оконешников, ответа на это, к сожалению, не даёт!
В сущности, автор просто-напросто нащупал такой НОВЫЙ способ, угадал, заметил СЛЕДСТВИЕ опледелённого НОВОГО ДЕЙСТВИЯ, а точнее - НОВОЕ свойство, такую форму действия (манипуляцию с цифрами) , которая и предопределила - не «математику формул», а. «математику действия».
Попробуем разобраться с механикой и содержанием этих авторских манипуляций.
- Нарисуем сначала Лимбы всех малых контейнеров (3х3) большой таблицы.
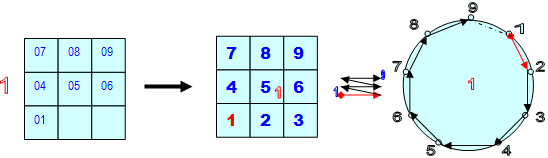 |
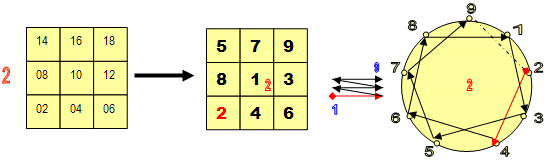 |
 |
 |
 |
 |
 |
 |
 |
ВЫВОДЫ:
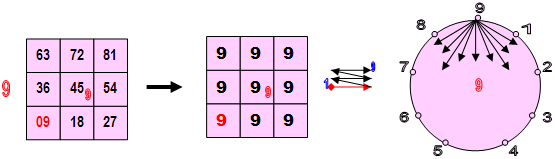
- Во-первых, с помощью Метода Лимбов нетрудно увидеть, что каждый из 9 «контейнеров» Большой таблица – малые таблички (3х3) это ничто иное, как развёрнутые КОДЫ саморепликации соответствующих (по месту в Большой таблице) Первоцифр
- Второе, что мы можем сказать, это то, что и в большой и в малых таблицах обход ячеек осуществляется «методом змейки» (слево – направо и снизу – вверх).
- Однако, результат умножения зависит от того, с какого контейнера мы начали умножение, то есть от того - каков будет МНОЖИТЕЛЬ, ибо внутренняя организация цифр (чисел) внутри каждого из контейнеров соответствует индивидуальной структуре внутреннего движения саморепликации соответствующей Первоцифры (см. лимбы каждого из контейнеров). А они – различны (и по направлению движения, и по характеру, и по частоте).
- Это означает, что конечный результат умножения существенно определяется МНОЖИТЕЛЕМ (у нас – цифрой «5»), его особенностями и свойствами, так как все дальнейшие процедуры действия не меняются.
- МНОЖИМОЕ же задаёт своими цифрами (каждая в своём разряде!) по сути дела ТРАЕКТОРИЮ ОБХОДА малой таблички, то есть является по сути дела – КОДОМ ОБХОДА малых квадратов (контейнеров).
- Этот КОД СЧИТЫВАНИЯ формирует тот самый набор ЧИСЕЛ, из которого далее будет получен искомый результат.
| Итак: Множитель – это «задатчик индивидуального типа действия (вида саморепликации), а Множимое – есть код обхода цифр саморепликации, своеобразная ВЫБОРКА из этих цифр(чисел) малой таблички. |
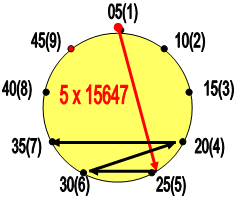
Сказанное выше можно графически отобразить рисунком абриса траектории на оцифрованном лимбе:
 |
А что означает наличие «выборочной» траектории из чисел, которые закономерно, в соответствии с собственным кодом (типом) саморепликации, имеют на лимбе свой порядок следования?
Цифра 5 имеет собственный код: 516273849, а код множимого, напомню = 15647.
Сравнив коды, видим, что совпадает только одна связь, да и та отличается своим противоположным направлением!
Согласно авторскому методу, результат умножения есть следствие процедуры сложения и выписывания (справа – налево) цифр Старшего разряда последнего числа с Младшим разрядом предыдущего Числа;
При этом крайние цифры остаются без изменения.
Будем манипулировать, как говорилось ранее, сслева – направо.
Тогда , результат будет такой:
5 (3+0) (2+0) (3+5) (2+5) – 532870. А теперь отразим данное число в зеркале – 078235!
| Стоит заметить, когда такого рода процедура (манипуляция) со связями чисел на лимбах, когда связи крайних чисел каждой пары чисел обозначаются, например, суммой цифры младшего разряда одного числа и цифрой старшего разряда другого числа, (причём, строго в направлениях обхода), то тогда такая процедура может быть самостоятельным Методом Анализа свойств чисел |
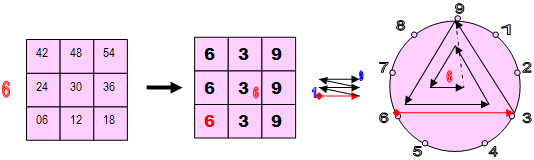
ОПЫТ 2: Апробация другого множителя
Следующим шагом нашего исследования мы посмотрим что получится, если множимое останется прежним (Число = 15647), а Множитель будет другим, например = 6.
Отличие этого Множителя в том, что он описывается циркулярным кодом: 639639639.
Как мы описывали выше, в нашей интерпретации код множителя (15647) указывает на то, какие числа надо выписать из соответствующей малой ячейки: получился набор чисел:
06-30-36-24-42.
Преобразуем этот набор, т.е расставим по-новому скобк, а затем сложим цифры в этих скобках: 0) (6-3)(0-3)(6-2)(4-4) (2 . В итоге получим число – 093882 = 93882.
Посмотрим на лимбы выполненной нами процедуры.
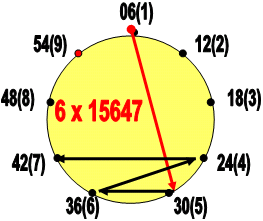 |
Траектория, задаваемая Множителем (а он остался прежним) не изменилась, но изменились числа, в узлах траектории, которые, естественно, принадлежат другому «контейнеру» - № 6.
Соответственно – поменяется и результат.
Попутно важно отметить, что собственный код нового Множителя (639639639) и код Множимомого (15647), в отличие от предыдущего опыта, абсолютно не совпадают!
То есть, всё дело и в числовом содержании (в оцифровке!)
Множителя, и в этой «хитрой процедуре» сложения разномастных разрядов соседних чисел, которые образуют (попарно) элементы траектории, заданной Множителем (см. рисунок ниже).
ОПЫТ 3: Так в чём же смысл «хитрой процедуры»?
Несмотря на разное содержание контейнеров-ячеек множителей и одинаковые (в наших примерах) коды обхода Множимого, Множители организованы по сходной схеме и по одному алгоритму.
Стало быть, в центр внимания отчётливо «вплывает» эта «хитрая процедура» попарного сложения чисел элемента траектории, когда (по ходу траектории) слагают цифры чисел по правилу: М+С (младший разряд 1-го числа со Старшим разрядом 2-го числа) или по правилу С+М, когда мы ведём счёт с другой стороны.
Индексация по правилу Оконешникова
А теперь попробуем использовать указанную процедуру для индексации собственно связей траектории на лимбе и проанализируем такой лимб.
Действуем по ходу траектории и пользуемся, значит, правилом – «М+С», откуда получаем такие индексы для элементов абриса (траектории), которые соответствуют результату умножения.
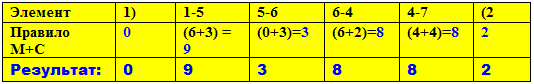 |
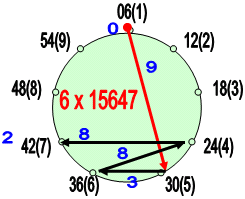 |
Из картинки выше можно сделать ещё ряд обобщений:
- Если некий лимб цифруенся (к примеру, по часовой стрелке) цифрами натурального ряда.
- Если рядом с этими цифрами проставляют (в порядке следования) числа развёрнутого кода одной из Первоцифр.
- Если затем, используя цифры первичной, натуральной оцифровки, на лимб наносят произвольную траекторию (отражающую некое число)
- И если осуществляют «хитрую процедуру» сложения разных разрядов попарных цифр элементов траекторми с выпистой таких сумм и добавлением крайних цифр (правило М+С, по ходу траектории)
- То тогда – всё проделанное – НОВЫЙ ВИД (способ) умножения НЕКОЕГО ЧИСЛА на заданную ПЕРВОЦИФРУ.
ОПЫТ 4: Если Множимое не есть таблица саморепликации…
А теперь представим себе следующее:
Пусть наш лимб (помимо натуральной оцифровки) оцифровывается НЕ ЧИСЛАМИ РАЗВЁРНУТОГО кода саморепликации Первоцифры, а иными, тоже развёрнутыми, числами, например, числами «саморепликации» двузначного или трёхзначного произвольного числа.
Пусть также «хитрая процедура» (даже с некоторыми усовершенствованиями) останется той же самой.
Вопрос: а будет ли тогда итог наших процедур (по своей сути) являться умножением?
Но, тогда возникает вопрос: а ЧЕМ будет /в арифметическом смысле/, результат счёта соответствующий «хитрой процедуре», если натуральный Лимб дополнительно оцифрован совершенно произвольным, но закономерным рядом одних чисел, а траектория на этом лимбе будет определена также произвольным, но другим законамерным кодом?
Будет ли в этом варианте результат - ВЗАИМНЫМ УМНОЖЕНИЕМ одного закогомерного процесса (кода) на другой закономерный процесс (код)?
Ответ здесь, по видимому, такой: «ДА», если только мы сумеем ПРАВИЛЬНО скорректировать (изменить, модифицировать) нашу «хитрую процедуру» счёта элементов траектории.
Последнее утверждение надо проверить на нескольких простых примерах.
ОПЫТ 5: Пусть Множитель не Первоцифра, а магический квадрат
Для начала пусть у нас по-прежнему Множителем будет какая-нибудь из Первоцифра, зато траекторию мы теперь зададим совсем «из другой оперыц», т.е. произвольно.
Эта траектория, в отличии от предыдущих, будет такова, что мы будем представление ясное о том, из чего она родилась.
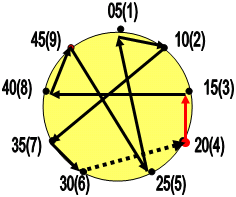
Поэтому выберем для нового эксперимента траекторию, заданную кодом обхода, например, магического квадрата Дюрера, причём, соблюдём общую закономерность и осуществим обход магического квадрата по той же «змейке», что и обход ячеек Первоцифр.
Итак:
- Лимб-9 цифруем как натурально, так и в соответствии с числами саморепликации цифры «5».
- Возьмём магический квадрат Дюрера:
- 3. Запишем код этого квадрата – 438951276
- 4. Нарисуем на лимбе красивую и симметричную траекторию кода магического квадрата:438951276, которая будет у нас МНОЖИМЫМ.
- Выпишем последовательность чисел внешней оцифровки связанных траекторией магического квадрата: 20-15-40-45-25-05-10-35-30
- По ходу траектории, как было написано выше, подготавлим ряд чисел под «хитрую процедуру»: 2) (0-1) (5-4) (0-4) (5-2) (5-0) (5-1) (0-3) (5-3) (0
- Произведём процедуру суммирования выделенных групп / с правого края/ 0,8,3,6,5,7,4,9,1,2 и зазеркалим полученное число и получим: 2194756380.
- Итог – число 2194756380;
- А мы и должны были получить такой результат: (5 х 438951276) = 2194756380
- Стало быть, умножения у нас получилось!
 |
 |
| Вывод: Если Множитель – код первоцифры на лимбе (с развёрнутой оцифовкой), а Множимое – код какой либо закономерности (по траектории обхода на квадрате), то специальная процедура Василия Оконешникова обеспечивает УМНОЖЕНИЕ кодов, а Лимбы дают графические образы результатов умножения. |
И как это выглядит визуально?
Чтобы посмотреть – снова отобразим НАШ результат (2194756380) на лимбе-9.
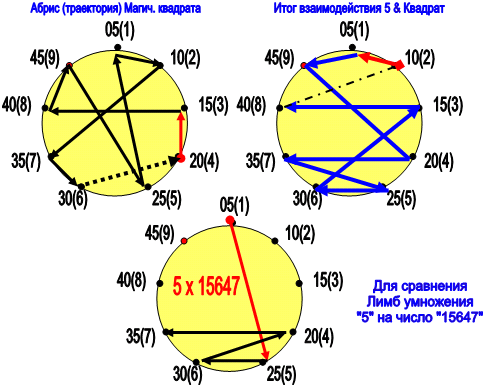 |
ОПЫТ 5: Пусть Множитель – табличка (и код) магического квадрата
А теперь исследуем «хитрую процедуру» счёта в новом варианте, когда вместо развёрнутого кода чисел, самореплицирующей Первоцифры «5» у нас будет иная закономерность, вписываемая в квадрат 3х3 и считываемая «змейкой».
Пусть в этом опыте в такой роли (Множителя) выступит такой же магический квадрат Дюрера, то есть будем рассчитывать на результат умножения 2-х магических квадратов
Итак, внвчале нарисуем Лимб 9 с оцифровками, соответствующими теперь магическому квадрату Дюрера:04(1)-03(2)-08(3)-09(4)-05(5)-01(6)-02(7)-07(8)-06(9)
 |
Теперь на оцифрованном лимбе обходом «змейка» рмсуем траекторию кода того же квадрата Дюрера (438951276)
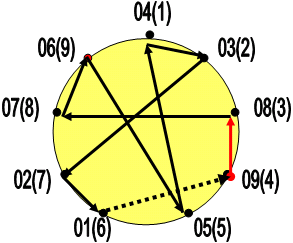 |
Далее выписываем оцифровки, на которые указывают узлы траектории на лимбе:
Подученный набор чисел заново группируем по правилу Оконешникова:
Крайние цифры не трогаем, а остальные /в скобказ/ складываем. Все эти действия производим справо – налево, чтобы потом взять зеркальный результат:
1234567890. Зеркало: 0987654321 или число - 987654321
Увы, как можно видеть, число полученного результата НЕ РАВНО ожидавшемуся правильному результату умножения:
|
Отсюда вывод:
МНОЖИМОЕ (при использовании процедуры Оконешникова) должно, по крайней мере, имитировать ту закономерность, которая присуща саморепликации и заложена в малых квадратах («контейнерах») большой таблицы.
Тогда, возможно, мы и получим УМНОЖЕНИЕ. |
ОПЫТ № 6 Множитель – саморепликация числа «12»
Исходя из вывода (см. выше) попробуем сконструировать некое Множимое по принципу саморепликации и заново произвести процедуру новоно умножения по правилу Оконешникова.
В качестве исходного числа, разумеется, нельзя брать Первоцифры. Поэтому возьмём, например, число 12.
Саморепликационный ряд (из 9 чисел) тогда будет такой: 12, 24, 36, 48, 60, 72, 84, 96,108.
Этот ряд можно разместить в искусственно сконструированной ячейке 3х3.
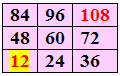 |
Теперь построим лимб из этих данных и произвести двойную оцифровку:
А затем нанести на полученный лимб траекторию кода магического квадрата Дюрера, то есть код - 438951276.
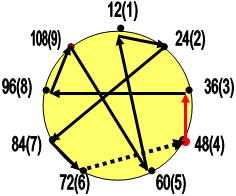 |
Теперь приступим к процедуре Оконешникова и выпишем оцифровки сконструированного квадрата (3х3) для числа 12, на которые указывают узлы траектории кода магического квадрата.
Осуществим перегруппировку этого набора:
(4 - 1) (1- 1) (5 – 1) (6- 1) (4 –0) (1- 0) (4 –1) (2 –1) (1) – 2
5 2 6 7 4 1 5 3 1 2 = 5267415312
Данный результат, по идее, должен соответствовать (в простом умножении)
12 х 438951276 = 5267415312, что мы и имеем!
|
ВЫВОД: Процедура «хитрого сложения» Оконешникова, заменяющая традиционное умножение, работает ТОЛЬКО со Множимым, имеющим саморепликационную структуру и вмещающимся в квадрат 3х3. Это содержимое (с двойной оцифровкой) формирует лимб, а на такой лимб можно вносить ЛЮБЫЕ траектории, соответствующие Множителю. |
Посмотрим, кстати, что представляет собой графически (на лимбе) результат умножения.
Итак, мы отображаем число – 5267415312. Получилось нечто не очень внятное, но … очевидное J!
Полученный абрис УМНОЖЕНИЯ Магического квадрата на число «12» можно далее подвергнуть числовому анализу, используя расширенную оцифровку, принадлежащую сконструированному нами саморепликационному квадрату числа «12».
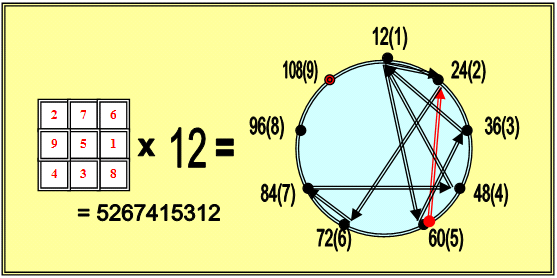 |